某企业为手机产业基地提供手机配件,受人民币走高的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
月份x
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
价格y1(元/件)
|
56
|
58
|
60
|
62
|
64
|
66
|
68
|
70
|
72
|
随着国家调控措施的出台,原材料价格的涨势趋缓,10至12月每件配件的原材料价格y2(元)与月份x(10≤x≤12,且x取整数)之间存在如图所示的变化趋势:
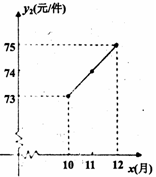
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1与x之间的函数关系式,根据如图所示的变化趋势,直接写出y2与x之间满足的一次函数关系式;
(2)若去年该配件每件的售价为100元,生产每件配件的人力成本为5元,其它成本3元,该配件在1至9月的销售量p1(万件)与月份x满足函数关系式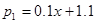 (1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式
(1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式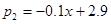 (10≤x≤12,且x取整数)。求去年哪个月销售该配件的利润最大,并求出这个最大利润;
(10≤x≤12,且x取整数)。求去年哪个月销售该配件的利润最大,并求出这个最大利润;
(3)今年1月,每件配件的原材料价格比去年12月上涨6元,人力成本比去年增加20%,其它成本没有变化,该企业将每件配件的售价在去年的基础上提高a%,与此同时1月份销售量在去年12月的基础上减少8a%,这样,在保证1月份上万件配件销量的前提下,完成了利润17万元的任务,请你计算出a的值。
 =
= (k≠0)与坐标轴分别交于A、B两点,OA、OB的长分别
(k≠0)与坐标轴分别交于A、B两点,OA、OB的长分别 =0的两根(OA>OB).动点P从O点出发,沿路线O→B→A以每
=0的两根(OA>OB).动点P从O点出发,沿路线O→B→A以每直接写出A、B两点的坐标;
设点P的运动时间为t(秒),△OPA的面积为S,求S与t之间的函数关系式;
当S=12时,求出点P的坐标,此时,在坐标轴上是否存在点M,使以O、A、


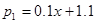 (1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式
(1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式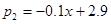 (10≤x≤12,且x取整数)。求去年哪个月销售该配件的利润最大,并求出这个最大利润;
(10≤x≤12,且x取整数)。求去年哪个月销售该配件的利润最大,并求出这个最大利润;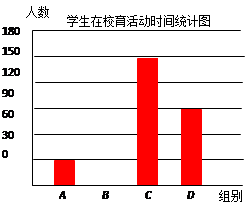
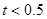
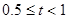
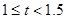
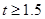
 :
: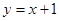 与直线
与直线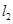 :
: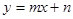 相交于点
相交于点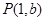 .
.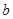 的值;
的值;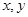 的方程组
的方程组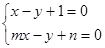 ,请你直接写出它的解。
,请你直接写出它的解。
 ,
, 的形式,又可以表示为0,
的形式,又可以表示为0, ,
,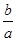 的形式,试求
的形式,试求 粤公网安备 44130202000953号
粤公网安备 44130202000953号