如图，在直角坐标系中，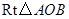
的两条直角边
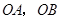分别在
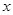轴的负半轴，
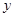轴的负半轴上，且
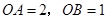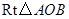．将绕点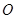
按顺时针方向旋转
，再把所得的像沿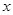轴正方向平移1个单位，得
．
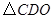（1）写出点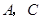
的坐标；
（2）求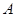点
和点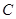
之间的距离．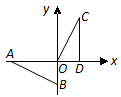
图为一位旅行者在早晨8时从城市出发到郊外所走的路程S（单位：千米）与时间t（单位：时）的变量关系的图象。根据图象回答问题：
（1）在这个变化过程中，自变量是 ，因变量是 。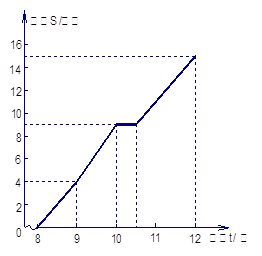
（2）9时，10时，12时所走的路程分别是多少？
（3）他休息了多长时间？
（4）他从休息后直至到达目的地这段时间的平均速度是多少？
已知变量y+1与（x－1）成反比例，且当x=2时，y=0.
（1）求y与x的函数关系式； （2）若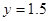
，求此时的x值.
已知直线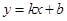
经过点
、
.
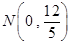（1）求直线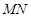
的解析式；
（2）当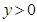
时，求
的取值范围；
（3）我们将横坐标、纵坐标均为整数的点称为整数点．直接写出此直线与两坐标轴围成的三角形的内部（不包含边界）的整数点的坐标．
在直角坐标系中，我们把横、纵坐标都为整数的点叫作整点.设坐标轴的单位长度为1cm，整点P从原点O出发，速度为1cm/s，且整点P作向上或向右运动，运动时间（s）与整点（个）的关系如下表：
| 整点P从原点O出发 的时间（s） |
可以得到整点P的坐标 |
可以得到整点 P的个数 |
| 1 |
（0，1），（1，0） |
2 |
| 2 |
（0，2），（1，1），（2，0） |
3 |
| 3 |
（0，3）（1，2）（2，1）（3，0） |
4 |
| … |
… |
… |
根据上表中的规律，回答下列问题：
⑴当整点P从点O出发4s时可得到的整点P有 个；
⑵当整点P从点O出发8s时，在直角坐标系中描出可以得到的整点，并顺次连接这些整点；
⑶当整点P从点O出发 s时，可以到达整点（16，4）的位置；
⑷当整点P（x,y）从点O出发30s时，当整点P（x,y）恰好在直线y＝2x－6上，求整点P的坐标.
小聪和小明沿同一条路同时从学校出发到图书馆查阅资料，学校与图书馆的路程是4千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达图书馆，图中折线O－A－B－C和线段OD分别表示两人离学校的路程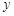
（千米）与所经过的时间
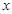（分钟）之间的函数关系，请根据图象回答下列问题：
（1）小聪在图书馆查阅资料的时间为 分钟，小聪返回学校的速度为 千米/分钟．
（2）请你求出小明离开学校的路程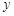(千米)与所经过的时间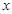(分钟)之间的函数关系；
（3）当小聪与小明迎面相遇时，他们离学校的路程是多少千米？
如图，奥运福娃在5×5的方格（每小格边长为1m）上沿着网格线运动．贝贝从A处出发去寻找B、C、D处的其它福娃，规定：向上向右走为正，向下向左走为负．如果从A到B记为：A→B（+1，+4），从B到A记为：B→A（-1，-4），其中第一个数表示左右方向，第二个数表示上下方向，那么图中
（1）A→C（___，___），B→C（___，___），C→（-3，-4）；
（2）若贝贝的行走路线为A→B→C→D，请计算贝贝走过的路程；
（3）若贝贝从A处去寻找妮妮的行走路线依次为（+2，+2），（-2，-1），（+2，+3），（-1，-2），请在图中标出妮妮的位置E点．
（4）在（3）中贝贝若每走1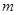
需消牦1．5焦耳的能量，则贝贝寻找妮妮过程中共需消耗多少焦耳的能量?
如图1，在平面直角坐标系xOy中，点A，B坐标分别为（8，4），（0，4），线段CD在于x轴上，CD＝3，点C从原点出发沿x轴正方向以每秒1个单位长度向右平移，点D随着点C同时同速同方向运动，过点D作x轴的垂线交线段AB于点E，交OA于点G，连结CE交OA于点F. 设运动时间为t，当E点到达A点时，停止所有运动.
（1）求线段CE的长；
（2）记S为RtΔCDE与ΔABO的重叠部分面积，试写出S关于t函数关系式及t的取值范围；
（3）如图2，连结DF，
1当t取何值时，以C，F，D为顶点的三角形为等腰三角形？
2直接写出ΔCDF的外接圆与OA相切时t的值.
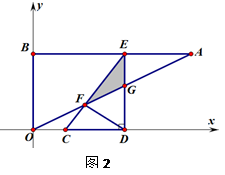
某单位准备印制一批证书，现有两个印刷厂可供选择，甲厂费用分为制版费和印刷费两部分，乙厂直接按印刷数量收取印刷费.甲、乙两厂的印刷费用y（千元）与证书数量x（千个）的函数关系图象分别如图中甲、乙所示.
(1) 请你直接写出甲厂的制版费及y甲与x的函数解析式，并求出其证书印刷单价.
(2) 当印制证书8千个时，应选择哪个印刷厂节省费用，节省费用多少元？
(3) 如果甲厂想把8千个证书的印制工作承揽下来，在不降低制版费的前提下，每个证书最少降低多少元？
甲、乙二人骑自行车同时从张庄出发，沿同一路线去李庄．甲行驶20分钟因事耽误一会儿，事后继续按原速行驶．下图表示甲、乙二人骑自行车行驶的路程y（千米）随时间x变化的图象（全程），根据图象回答下列问题：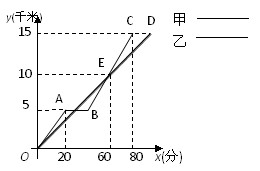
（1）乙比甲晚多长时间到达李庄？
（2）甲因事耽误了多长时间？
（3）x为何值时，乙行驶的路程比甲行驶的路程多1千米？
图为一位旅行者在早晨８时从城市出发到郊外所走的路程S（单位：千米）与时间t（单位：时）的变量关系的图象。根据图象回答问题：
在这个变化过程中，自变量是____，因变量是______。
９时，１０时３０分，１２时所走的路程分别是多少？
他休息了多长时间？
他从休息后直至到达目的地这段时间的平均速度是多少？
如图，在以O为原点的平面直角坐标系中，点A、C分别在x轴、y轴的正半轴上，点B(a，b)在第一象限，四边形OABC是矩形，反比例函数y＝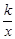
（k>0，x>0）的图象与AB相交于点D，与BC相交于点E，且BE＝CE．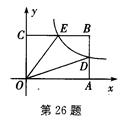
试说明：BD＝AD；
若四边形ODBE的面积是9，求k的值．
已知某种水果的批发单价与批发量的函数关系如图（1）所示．请说明图中①、②两段函数图象的实际意义．
写出批发该种水果的资金金额w（元）与批发量m（kg）之间的函数关系式；在下图的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果
经调查，某经销商销售该种水果的日最高销量与零售价之间的函数关系如图（2）所示，该经销商拟每日售出60kg以上该种水果，且当日零售价不变，请你帮助该经销商设计进货和销售的方案，使得当日获得的利润最大．
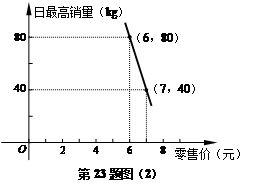
已知正比例函数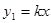
(k≠0)和反比例函数
的图象都经过点(－2，1)．求这两个函数的表达式；
试说明当x为何值时，
的图象与边BC交于点F。
的值：
粤公网安备 44130202000953号