已知某种水果的批发单价与批发量的函数关系如图(1)所示.请说明图中①、②两段函数图象的实际意义.


写出批发该种水果的资金金额w(元)与批发量m(kg)之间的函数关系式;在下图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果
经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图(2)所示,该经销商拟每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.

相关知识点
推荐套卷
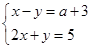 的解x、y满足x>0.y<0求a的取值范围.
的解x、y满足x>0.y<0求a的取值范围. (1)
(1)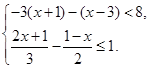 (2)
(2) 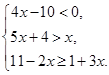
 ≤9.
≤9.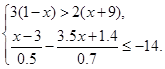
 12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000
12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000 和乙种板材12000
和乙种板材12000 两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间
两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间 型板房和一间
型板房和一间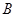 型板房所需板材及能安置的人数如下表所示:
型板房所需板材及能安置的人数如下表所示: ,
,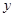 的方程组
的方程组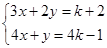 的解
的解 ,求
,求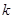 的取值范围.
的取值范围.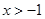 ;⑵
;⑵ ;⑶
;⑶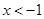 ;⑷
;⑷ ;⑸
;⑸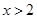 且
且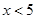
 粤公网安备 44130202000953号
粤公网安备 44130202000953号