已知,点P(x,y)在第一象限,且x+y=12,点A(10,0)在x轴上,设△OPA的面积 为S.求S关于x的关系式,并确定x的取值范围;
当△OPA为直角三角形时,求P点的坐标.

如图,A是反比例函数 图象上一点,过点A作AB⊥x轴于点B,点P在y轴上,△ABP的面积为1,则k的值为( )
图象上一点,过点A作AB⊥x轴于点B,点P在y轴上,△ABP的面积为1,则k的值为( )
| A.1 | B.2 | C.-1 | D.-2 |

下列函数中,y一定随x的增大而减小的是 ( ▲ )
| A.y=-5x2(x>1) | B.y=-2+3x | C.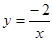 |
D.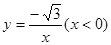 |
竖直向上发射的小球的高度h(m)关于运动时间t(s)的函数解析式为h=at2+bt,若小球在发射后第3秒与第9秒时的高度相等,则下列时刻中小球的高度最高的是( ▲)
A、第4.2秒 B第5.8秒 C、6.4秒 D、第7.1秒
下列各函数中,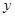 随
随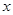 增大而增大的是( )
增大而增大的是( )
①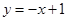 . ②
. ② (x < 0) ③
(x < 0) ③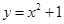 . ④
. ④

| A.①② | B.②③ | C.②④ | D.①③ |
如图,在Rt△ABC中,∠C=90°,AB=5cm,BC=3cm,动点P从点A 出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止.设y=PC2,运动时间为t秒,则能反映y与t之间函数关系的大致图象是 【▲】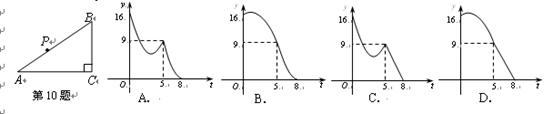
小颖从家出发,走了20分钟,到一个离家1000米的图书室,看了40分钟的书后,用15分钟返回到家,图(3)中表示小颖离家时间x与距离y之间的关系正确的是( )
如图,一只小虫在折扇上沿O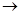 A
A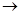 B
B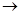 O路径匀速爬行,能大致描述小虫距出发点O的距离y与时间x之间的函数图象是
O路径匀速爬行,能大致描述小虫距出发点O的距离y与时间x之间的函数图象是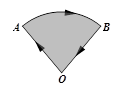
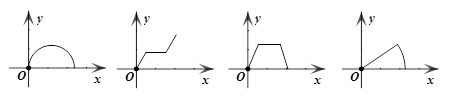
(A) (B) (C) (D)
下图是韩老师早晨出门散步时,离家的距离y与时间x的函数图象.若用黑点表示韩老师家的位置,则韩老师散步行走的路线可能是------------------------------( )
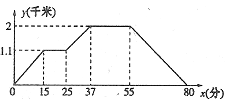
如图反映的过程是:小强从家去菜地浇水,又去玉米地除草,然后回家.如果菜地和玉米地的距离为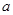 千米,小强在玉米地除草比在菜地浇水多用的时间为b分钟,则
千米,小强在玉米地除草比在菜地浇水多用的时间为b分钟,则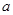 ,b的值分别为( )
,b的值分别为( )
| A.1.1,8 | B.0.9,3 |
| C.1.1,12 | D.0.9,8 |