[江苏]2012届江苏盐城亭湖区九年级下学期第一次调研考试数学试卷
世界文化遗产长城总长约6700000 ,用科学记数法可表示为 ( )
,用科学记数法可表示为 ( )
A.6.7×105 |
B.6.7×10-5 |
C.6.7×106 |
D.6.7×10-6 |
若反比例函数 的图象经过点(-1,2),则这个函数的图象一定经过点( )
的图象经过点(-1,2),则这个函数的图象一定经过点( )
| A.(2,-1) | B.( ,2) ,2) |
C.(-2,-1) | D.( ,2) ,2) |
亭湖区于3月中旬进行了初三英语口语测试模拟考试,王老师为了了解他所教的甲、乙两个班学生英语口语测验成绩哪一班比较整齐,通常需要知道两个班成绩的( )
| A.平均数 | B.方差 | C.众数 | D.频率分布 |
如果圆柱的母线长为5cm,底面半径为2cm,那么这个圆柱的侧面积是( )
A、 B、
B、 C、
C、 D、
D、
一次函数y=2x+3的图象沿 轴向下平移2个单位,所得图象的函数解析式是( )
轴向下平移2个单位,所得图象的函数解析式是( )
| A.y=2x-3 | B.y=2x+2 | C.y=2x+1 | D.y=2x |
要在一个矩形纸片上画出半径分别是9cm和4cm的两个外切圆,该矩形纸片面积的最小值是( )。
| A. 468 | B.450 | C. 396 | D.225 |
如图2,
请根据图中给出的信息,可得正确的方程是( )
A.π× x=π× x=π× ×(x+5) ×(x+5) |
B.π× x=π× x=π× ×(x-5) ×(x-5) |
| C.π×82×x=π×62×(x+5) | D.π×82×x=π×62×5 |
观察下列各式:(x-1) (x+1)=x2-1;(x-1)(x2+x+1)=x3-1;(x-1)(x3+x2+x+1)=x4-1;…;根据前面各式的规律可得到(x-1)(xn+xn-1+xn-2+…+x+1)=
如图4,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当CM= 时,△AED与以M、N、C为顶点的三角形相似
如图5,数轴上表示1、 的对应点分别为A、B,点B关于点A的对称点为C,则点C所表示的数是 。
的对应点分别为A、B,点B关于点A的对称点为C,则点C所表示的数是 。
如图6,一张桌子上摆放着若干个碟子,从三个方向看,三种视图如下图所示,则这张桌子上共有碟子 个。
|

如图7,是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1,A2,A3,….若从O点到A1点的回形线为第1圈(长为7),从A1点到A2点的回形线为第2圈,…,依此类推.则第20圈的长为 。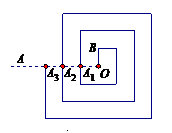
如图8,△ABC中,AB=AC,若点D在AB上,点E在AC上,请你加上一个条件,使结论BE=CD成立,同时补全图形,并证明此结论
如图9,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后, 的顶点均在格点上,坐标为A(1,-4),B(5,-4),C
的顶点均在格点上,坐标为A(1,-4),B(5,-4),C .
.
作出
 关于
关于 轴对称的
轴对称的 ,并写出点
,并写出点 的对称点
的对称点 的坐标;
的坐标;作出
 关于原点
关于原点 对称的
对称的 ,并写出点
,并写出点 的对称点
的对称点 的坐标
的坐标试判断:
 与
与 是否关于
是否关于 轴对称(只需写出判断结果)。
轴对称(只需写出判断结果)。
北京08奥运会吉祥物是“贝贝、晶晶、欢欢、迎迎、妮妮”.现将三张分别印有“欢欢、迎迎、妮妮”这三个吉祥物图案的卡片(卡片的形状大小一样,质地相同)放入盒子。
小明从盒子中任取一张,取到卡片欢欢的概率是多少?
小明从盒子中取出一张卡片,记下名字后放回,再从盒子中取出第二张卡片,记
下名字。用列表或画树状图列出小明取到的卡片的所有可能情况,并求出两次都取到卡
片欢欢的概率
如图10,已知⊙O的直径AB垂直于弦CD,垂足为E,F为CD延长线上一点,AF交⊙O于点G. 求证:AC2=AG·AF
在形如 的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫做对数运算。
定义:如果 (a>0,a≠1,N>0),则b叫做以a为底N的对数,记作:
(a>0,a≠1,N>0),则b叫做以a为底N的对数,记作: ,例如:求
,例如:求 ,因为
,因为 =8,所以
=8,所以 =3;又比如∵
=3;又比如∵ ,∴
,∴ .
.根据定义计算:(本小题6分)
① =____;②
=____;② = ;
= ;
③如果 ,那么x= 。
,那么x= 。设
 则
则 (a>0,a≠1,M、N均为正数),
(a>0,a≠1,M、N均为正数),
∵ ,∴
,∴ ∴
∴ ,
,
即
这是对数运算的重要性质之一,进一步,我们还可以得出: = .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
= .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)请你猜想:
 (a>0,a≠1,M、N均为正数).(本小题2分)
(a>0,a≠1,M、N均为正数).(本小题2分)
如图11,已知○为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
求点B的坐标
若二次函数y=ax+bx+c的图象经过A、B、O三点,求此二次函数的解析式;
在(2)中的二次函数图象的OB段(不包括点O、B)上,是否存在一点C,使得四边形ABCO的面积最大?若存在,求出这个最大值及此时点C的坐标;若不存在,请说明理由。


 中自变量
中自变量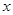 的取值范围是
的取值范围是  的值为-5时,则输出的数值为 。
的值为-5时,则输出的数值为 。
 并把解集在数轴上表示出来
并把解集在数轴上表示出来
 ,其中x=
,其中x=  .
. ,AC=BC=2,M是边AC的中点,CH⊥BM于H.
,AC=BC=2,M是边AC的中点,CH⊥BM于H.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号