如图11，已知○为坐标原点，∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).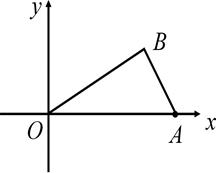
求点B的坐标
若二次函数y=ax+bx+c的图象经过A、B、O三点，求此二次函数的解析式；
在(2)中的二次函数图象的OB段(不包括点O、B)上，是否存在一点C，使得四边形ABCO的面积最大？若存在，求出这个最大值及此时点C的坐标；若不存在，请说明理由。
相关试题
如图，二次函数的图象与
轴交于A（-3，0）和B（1，0）两点，交
轴于点C（0，3），点C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D．
（1）请直接写出D点的坐标．
（2）求二次函数的解析式．
（3）根据图象直接写出使一次函数值大于二次函数值的的取值范围．
山西特产专卖店销售核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每降低2元，则平均每天的销售可增加20千克，若该专卖店销售这种核桃要想平均每天获利2240元，请回答：
（1）每千克核桃应降价多少元？
（2）在（1）问的条件下，平均每天获利不变，为尽可能让利于顾客，赢得市场，该店应按原售价的几折出售？
（3）写出每天总利润
与降价
元的函数关系式，为了使每天的利润最大，应降价多少元？
把一副扑克牌中的三张黑桃牌（它们正面的数字分别为3,4,5）洗匀后正面朝下放在桌面上．小王和小李玩摸牌游戏，游戏规则如下：先由小王随机抽取一张牌，记下牌面数字后放回，洗匀后正面朝下，再由小李随机抽取一张牌，记下牌面数字．当两张牌的牌面数字相同时，小王赢；当两张牌的牌面数字不同时，小李赢．
（1）请利用画树状图或列表的方法表示出所有可能出现的结果；
（2）分析游戏规则对双方是否公平，并说明理由．
经过点A（-2,-8）．
相关知识点
推荐套卷
粤公网安备 44130202000953号