[浙江]2012届浙江省绍兴市六所名校初中毕业生学业考试三模数学卷

下列各组数中，互为相反数的是（　▲　）

A．2和﹣2

B．﹣2和

C．﹣2和﹣

D．和2

下列运算中，结果正确的是（ ▲ ）                                             

A．

B．

C．

D．

下面四个几何体中，主视图与其它几何体的主视图不同的是（　▲　）

如图，已知直线AB∥CD，∠C＝115°，∠A＝25°，则∠E＝(  ▲  )

已知⊙O₁和⊙O₂的半径分别为2cm和5cm，两圆的圆心距是3.5cm，则两圆的位置关系是（ ▲ ）

如图，如果从半径为9cm的圆形纸片剪去圆周的一个扇形，将留下的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的高为（▲ ）

A．6cm

B．cm

C．8cm

D．cm

如图，在网格的两个格点上摆放黑、白两个棋子，使两棋子不在同一条格线上．其中恰好如图示位置摆放的概率是（ ▲ ）

A．

B．

C．

D．

下列函数中，y一定随x的增大而减小的是 （ ▲ ）

A．y=-5x2(x>1)

B．y=-2+3x

C．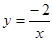

D．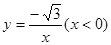

如图，已知A、B两点的坐标分别为(－2，0)、(0，1)，⊙C的圆心坐标为(0，－1)，半径为1．若D是⊙C上的一个动点，射线AD与y轴交于点E，则△ABE面积的最大值是（ ▲ ）

A．3      B．    C．     D．4

已知抛物线，且满.则称抛物线互为“友好抛物线”，则下列关于“友好抛物线”的说法不正确的是（ ▲ ）

在日本核电站事故期间，我国某监测点监测到极微量的人工放射性核素碘－131，其深度为0.0000963贝克/立方米.数据“0.0000963”用科学记数法可表示为   ▲   ．

因式分解 =____ ▲ ．

经过点（－2,3）的直线y=kx+b与直线y=3x-2平行，则该直线的解析式是   ▲   ．

双曲线、在第一象限的图像如图，，过上的任意一点，作轴的平行线交于, 交轴于，若，则的解析式是_  ▲ .                                      

如图，点D、E分别在∠ABC的边BC、AB上，过D、A、C三点的圆的圆心为E，过B、E、F三点的圆的圆心为D，如果∠A="63" º，设，那么=   ▲  º．

在直角梯形OABC中，OA∥BC，A、B两点的坐标分别为A（13，0），B（11，12），动点P、Q同时从O、B两点出发，点P以每秒2个单位的速度沿OA向终点A运动，点Q以每秒1个单位的速度沿BC向C运动，当点P停止运动时，点Q同时停止运动.线段OB、PQ相交于点D，过点D作DE∥OA，交AB于点E，射线QE交轴于点F（如图）.设动点P、Q运动时间为t（单位：秒），则：

（1）当t＝  ▲  时，四边形PABQ是平行四边形；
（2）当t＝  ▲  时，△PQF是等腰三角形．

（1）计算： 
(2)先化简：·，然后再取一个你喜爱的的值代入求值．

如图，C是线段AB的中点，CD平分∠ACE，CE平分∠BCD，CD=CE

(1)求证：△ACD≌△BCE；
(2)若∠D=50°，求∠B的度数．

一辆轿车在如图的公路上匀速行驶，该轿车在11∶20从A地出发，到相距50km的B地办事．

（1）若车速为60km/h，问该轿车到达B地的时间？
（2）若要求在12∶00之前到达B地，问该轿车的车速应在什么范围内？

我们都知道主动吸烟和被动吸烟都危害着人类的健康．为此，联合国规定每年的5月31日为“世界无烟日”．为配合今年的“世界无烟日”宣传活动，我区某校九年级二班的同学们在城区内开展了以“我支持的戒烟方式”为主题的问卷调查活动，征求居民的意见，并将调查结果分析整理后，制成了如下统计图：

(1)求九年级二班的同学们一共随机调查了多少人？
(2)根据以上信息，请你把统计图补充完整；
(3)如果城区有2万人，那么请你根据以上调查结果，估计城区大约有多少人支持“强制戒烟”这种戒烟方式？
（4）为了青少年的健康，请你提出一条你认为最有效的戒烟措施.

放风筝是大家喜爱的一种运动．星期天的上午小明在大洲广场上放风筝．如图他在A处时不小心让风筝挂在了一棵树的树梢上，风筝固定在了D处．此时风筝线AD与水平线的夹角为30°． 为了便于观察．小明迅速向前边移动边收线到达了离A处7米的B处，此时风筝线BD与水平线的夹角为45°．已知点A、B、C在同一条直线上，∠ACD=90°．请你求出小明此吋所收回的风筝线的长度是多少米？（本题中风筝线均视为线段，≈1.414，≈1.732．最后结果精确到1米）

在函数中,我们把关于x的一次函数与称为一对交换函数，如与是一对交换函数.称函数是函数的交换函数.
（1）求函数y＝x＋4与交换函数的图像的交点坐标；    
（2）若函数y＝x＋b（b为常数）与交换函数的图像及纵轴所围三角形的面积为4,求b 的值．

已知∠ABC=90°，点P为射线BC上任意一点（点P与点B不重合），分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连结QE并延长交BP于点F.

（1）如图1，若AB=，点A、E、P恰好在一条直线上时，求此时EF的长（直接写出结果）；
（2）如图2，当点P为射线BC上任意一点时，猜想EF与图中的哪条线段相等（不能添加辅助线产生新的线段），并加以证明；
（3）若AB=，设BP=4，求QF的长．

如图，二次函数与x轴交于A、B两点，与y轴交于C点，点P从A点出发，以1个单位每秒的速度向点B运动，点Q同时从C点出发，以相同的速度向y轴正方向运动，运动时间为t秒，点P到达B点时，点Q同时停止运动。设PQ交直线AC于点

（1）求直线AC的解析式；
（2）设△PQC的面积为S，求S关于t的函数解析式；
（3）在y轴上找一点M，使△MAC和△MBC都是等腰三角形。直接写出所有满足条件的M点的坐标；
（4）过点P作PE⊥AC，垂足为E，当P点运动时，线段EG的长度是否发生改变，请说明理由。