已知∠ABC=90°，点P为射线BC上任意一点（点P与点B不重合），分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连结QE并延长交BP于点F.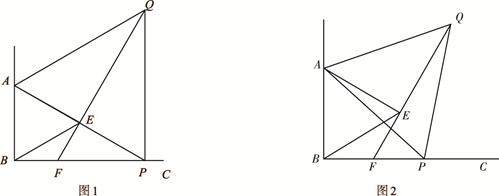
（1）如图1，若AB=
，点A、E、P恰好在一条直线上时，求此时EF的长（直接写出结果）；
（2）如图2，当点P为射线BC上任意一点时，猜想EF与图中的哪条线段相等（不能添加辅助线产生新的线段），并加以证明；
（3）若AB=，设BP=4，求QF的长．
相关试题
（如图），试取斜边
上的一点为圆心画图，使点
，
，
分别在所画的圆内、圆外和圆上．
，连结
，
相交于点
，以点
为圆心，
cm长为半径画圆，试判断点
，
，
，
中，
，求证
，
，
，
四个顶点共圆．相关知识点
推荐套卷
粤公网安备 44130202000953号