我们常用“水滴石穿”来说明一个人只要持之以恒地做某件事,就一定能成功.经测算,当水滴不断地滴在一块石头上时,经过10年,石头上可形成一个深为1厘米的小洞,那么平均每个月小洞的深度增加多少米?(结果保留三个有效数字,并用科学记数法表示)
设a,b是任意两个实数,规定a与b之间的一种运算“⊕”为: ,
例如: ,
(因为 )
参照上面材料,解答下列问题:
(1) , ;
(2)若 ,且满足 ,求x的值.
已知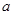 、
、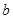 互为相反数且
互为相反数且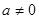 ,
, 、
、 互为倒数,
互为倒数,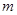 的绝对值是最小的正整数,
的绝对值是最小的正整数,
求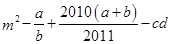 的值. (注:
的值. (注: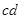 =
=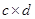 )
)
解:∵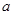 、
、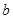 互为相反数且
互为相反数且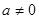 , ∴
, ∴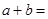 __________,
__________, __________;
__________;
又∵ 、
、 互为倒数,∴
互为倒数,∴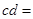 __________;
__________;
又∵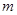 的绝对值是最小的正整数, ∴
的绝对值是最小的正整数, ∴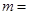 __________,∴
__________,∴ __________;
__________;
∴原式 __________.
__________.
计算:
(1)7÷(-  )×(
)×( -
-  );
);
(2)2a-3b+[4a-(3a-b)];
(3)(-x2)4+x3·x5-(3x4)2;
(4)(-  )-1+(-2)2×50;
)-1+(-2)2×50;
观察下列等式
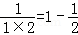 ,
,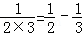 ,
,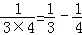 ,
,
将以上三个等式两边分别相加得:
 =1﹣
=1﹣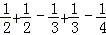 =1﹣
=1﹣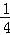 =
= .
.
(1)猜想并写出: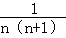 .
.
(2)根据以上规律直接写出下列各式的计算结果:
①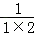 +
+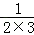 +
+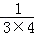 +…+
+…+ = ;
= ;
②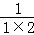 +
+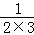 +
+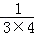 +…+
+…+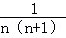 .
.
(3)探究并计算: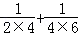 +
+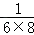 +…+
+…+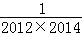 .
.
我们知道,任意一个正整数 都可以进行这样的分解: , 是正整数,且 ,在 的所有这种分解中,如果 , 两因数之差的绝对值最小,我们就称 是 的最佳分解.并规定: .例如12可以分解成 , 或 ,因为 ,所以 是12的最佳分解,所以 .
(1)如果一个正整数 是另外一个正整数 的平方,我们称正整数 是完全平方数.求证:对任意一个完全平方数 ,总有 ;
(2)如果一个两位正整数 , , , 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数 为"吉祥数",求所有"吉祥数"中 的最大值.
甲、乙两商场上半年经营情况如下(“+”表示盈利,“-”表示亏本,以百万为单位)
| 月份 |
一 |
二 |
三 |
四 |
五 |
六 |
| 甲商场 |
+0.8 |
+0.6 |
-0.4 |
-0.1 |
+0.1 |
+0.2 |
| 乙商场 |
+1.3 |
+1.5 |
-0.6 |
-0.1 |
+0.4 |
-0.1 |
(1)三月份乙商场比甲商场多亏损多少元?
(2)六月份甲商场比乙商场多盈利多少元?
(3)甲、乙两商场上半年平均每月分别盈利或亏损多少元?
阅读以下材料:
苏格兰数学家纳皮尔 . , 年)是对数的创始人.他发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉 , 年)才发现指数与对数之间的联系.
对数的定义:一般地,若 且 ,那么 叫做以 为底 的对数,记作 ,比如指数式 可以转化为对数式 ,对数式 可以转化为指数式 .
我们根据对数的定义可得到对数的一个性质:
, , , ,理由如下:
设 , ,则 , ,
,由对数的定义得 .
又 ,
.
根据上述材料,结合你所学的知识,解答下列问题:
(1)填空:① ,② ,③ ;
(2)求证: , , , ;
(3)拓展运用:计算 .
观察以下等式:
第1个等式: ,
第2个等式: ,
第3个等式: ,
第4个等式: .
第5个等式: .
按照以上规律,解决下列问题:
(1)写出第6个等式: ;
(2)写出你猜想的第 个等式: (用含 的等式表示),并证明.
用※定义一种新运算:对于任意实数 和 ,规定 ※ ,如:1※ .
(1)求 ※ ;
(2)若3※ ,求 的取值范围,并在所给的数轴上表示出解集.
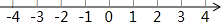
已知两个有理数: 和5.
(1)计算: ;
(2)若再添一个负整数 ,且 ,5与 这三个数的平均数仍小于 ,求 的值.