初中数学有理数的混合运算解答题

有个填写运算符号的游戏：在“1□2□6□9”中的每个□内，填入，，，中的某一个（可重复使用），然后计算结果．

（1）计算：；

（2）若□，请推算□内的符号；

（3）在“1□2□”的□内填入符号后，使计算所得数最小，直接写出这个最小数．

为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的收费标准如下表：

例如：某户居民1月份用水8立方米，应收水费为2×6+4×（8-6）=20（元）．
请根据上表的内容解答下列问题：
（1）若某户居民2月份用水5立方米，则应收水费多少元？
（2）若某户居民3月份交水费36元，则用水量为多少立方米？
（3）若某户居民4月份用水a立方米（其中6＜a＜10），请用含a的代数式表示应收水费．
（4）若某户居民5、6两个月共用水18立方米（6月份用水量超过了10立方米），设5月份用水x立方米，请用含x的代数式表示该户居民5、6两个月共交水费多少元．

规定*是一种运算符号，且a*b=ab－2a，试计算4*（－2*3）．

仔细观察下列三组数：
第一组：1，4，9，16，25，…
第二组：1，8，27，64，125，…
第三组：﹣2，﹣8，﹣18，﹣32，﹣50，…
（1）写出每组的第6个数各是多少？
（2）第二组的第100个数是第一组的第100个数的多少倍？
（3）取每组数的第n个数，计算这三个数的和．

在" $-$ "" $\times$ "两个符号中选一个自己想要的符号，填入 $2^2+2\times (1$ □ $\frac{1}{2})$ 中的□，并计算．

有一批水果，包装质量为每筐25千克，现抽取10筐样品进行检测，结果称重如下（单位：千克）：21，24，27，28，25，26，22，23，25，26为了求得10筐样品的总质量，我们可以选取一个恰当的基准数进行简化运算．

原质量	21	24	27	28	25	26	22	23	25	26
与基准数的差距

 
（1）你认为选取的一个恰当的基准数为____________；
（2）根据你选取的基准数，用正、负数填写上表；
（3）这10筐水果的总质量是多少千克？

出租车司机小李某天下午的营运全是在东西走向的人民大街上进行的，如果规定向东为正，向西为负，他这天下午行车里程（单位：千米）如下：+15，－2．5，+5，－1，+10．5，－3，－2，+12，+4，－5，+6．
（1）若小李出发地记为0，他将最后一名乘客送抵目的地小李距出发地点有多远？
（2）若汽车耗油量为0．4升/ 千米，这天下午小李共耗油多少升？

下图是一个数字转换机，请解答下列问题：

（1）填空：若输入的x值为2，则输出的y值为          
（2）若输入的x值为1，则输出的y值为          
（3）若输出的y值为28，那么输入的x值是什么？（写出三个x值，并写出简要的分析过程．）

某工艺厂计划一周生产工艺品2100个，平均每天生产300个，但实际每天生产量与计划相比有出入．下表是某周的生产情况（超产记为正、减产记为负）：

星期	一	二	三	四	五	六	日
增减（单位：个）	＋5	－2	－5	+15	－10	+16	－9

 
（1）写出该厂星期一生产工艺品的数量；
（2）本周产量中最多的一天比最少的一天多生产多少个工艺品？
（3）请求出该工艺厂在本周实际生产工艺品的数量；
（4）已知该厂实行每周计件工资制，每生产一个工艺品可得60元，若超额完成任务，则超过部分每个另奖50元，少生产一个扣80元．试求该工艺厂在这一周应付出的工资总额．

阅读以下材料：

苏格兰数学家纳皮尔 $(J$． $\mathit{Npler}$， $1550-1617$年）是对数的创始人．他发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉 $(\mathit{Evler}$， $1707-1783$年）才发现指数与对数之间的联系．

对数的定义：一般地，若 $a^x=N(a>0$且 $a\ne 1)$，那么 $x$叫做以 $a$为底 $N$的对数，记作 $x={\log }_{a}N$，比如指数式 $2^4=16$可以转化为对数式 $4={\log }_{2}16$，对数式 $2={\log }_{3}9$可以转化为指数式 $3^2=9$．

我们根据对数的定义可得到对数的一个性质：

${\log }_a(M\cdot N)={\log }_{a}M+{\log }_{a}N(a>0$， $a\ne 1$， $M>0$， $N>0)$，理由如下：

设 ${\log }_{a}M=m$， ${\log }_{a}N=n$，则 $M=a^m$， $N=a^n$，

$\therefore M\cdot N=a^m\cdot a^n=a^{m+n}$，由对数的定义得 $m+n={\log }_a(M\cdot N)$．

又 $\because m+n={\log }_{a}M+{\log }_{a}N$，

$\therefore {\log }_a(M\cdot N)={\log }_{a}M+{\log }_{a}N$．

根据上述材料，结合你所学的知识，解答下列问题：

（1）填空：① ${\log }_{2}32=$　　，② ${\log }_{3}27=$　　，③ ${\log }_{7}1=$　　；

（2）求证： ${\log }_a\frac{M}{N}={\log }_{a}M-{\log }_{a}N(a>0$， $a\ne 1$， $M>0$， $N>0)$；

（3）拓展运用：计算 ${\log }_{5}125+{\log }_{5}6-{\log }_{5}30$．

观察以下等式：

第1个等式： $\frac{1}{3}\times (1+\frac{2}{1})=2-\frac{1}{1}$，

第2个等式： $\frac{3}{4}\times (1+\frac{2}{2})=2-\frac{1}{2}$，

第3个等式： $\frac{5}{5}\times (1+\frac{2}{3})=2-\frac{1}{3}$，

第4个等式： $\frac{7}{6}\times (1+\frac{2}{4})=2-\frac{1}{4}$．

第5个等式： $\frac{9}{7}\times (1+\frac{2}{5})=2-\frac{1}{5}$．

$\dots$

按照以上规律，解决下列问题：

（1）写出第6个等式：　 $\frac{11}{8}\times (1+\frac{2}{6})=2-\frac{1}{6}$　；

（2）写出你猜想的第 $n$个等式：　　（用含 $n$的等式表示），并证明．

用※定义一种新运算：对于任意实数 $m$ 和 $n$ ，规定 $m$ ※ $n=m^{2}n-\mathit{mn}-3n$ ，如：1※ $2=1^2\times 2-1\times 2-3\times 2=-6$ ．

（1）求 $(-2)$ ※ $\sqrt{3}$ ；

（2）若3※ $m⩾-6$ ，求 $m$ 的取值范围，并在所给的数轴上表示出解集．

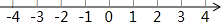
已知两个有理数： $-9$ 和5．

（1）计算： $\frac{(-9)+5}{2}$ ；

（2）若再添一个负整数 $m$ ，且 $-9$ ，5与 $m$ 这三个数的平均数仍小于 $m$ ，求 $m$ 的值．

某地区高山的温度从山脚开始每升高100m降低0．6℃，现测得山脚的温度是4℃．
（1）求离山脚1200m高的地方的温度．
（2）若山上某处气温为-5℃，求此处距山脚的高度．

观察下列各式：
1³+2³=；
1³+2³+3³=36=；
1³+2³+3³+4³=100=；
（1）计算：1³+2³+3³+4³+5³的值；
（2）计算：1³+2³+3³+4³+…+10³的值；
（3）猜想：1³+2³+3³+4³+…+n³的值．