如图所示,某战役 缴获敌人
缴获敌人 防御工事坐标地图碎片,依稀可见:一号暗堡的坐标为(4,2),四号暗堡的坐标为(-2,2)。另有情报得知:指挥部坐标为(0,0),你认为敌军指挥部的位置大约是( )
防御工事坐标地图碎片,依稀可见:一号暗堡的坐标为(4,2),四号暗堡的坐标为(-2,2)。另有情报得知:指挥部坐标为(0,0),你认为敌军指挥部的位置大约是( )
| A.A处 | B.B处 | C.C处 | D.D处 |
.下列现象中,属于平移现象的为( )
| A.方向盘的转动 | B.自行车行驶时车轮的转动 | C.钟摆的运动 | D.电梯的升降 |
用科学计数法表示的树-3.6×10-4写成小数是( )
A 0.00036 B -0.0036 C -0.00036 D -36000
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点. 
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD
向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于E
①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?
②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?
请直接写出相应的t值.
一个袋中有3张形状大小完全相同的卡片,编号为1,2,3,先任取一张,将其编号记为m,再从剩下的两张中任取一张,将其编号记为n.
(1)请用树状图或者列表法,表示事件发生的所有可能情况;
(2)求关于x的方程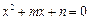 有两个不相等实数根的概率.
有两个不相等实数根的概率.
如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,如果水位上升3米,则水面CD的宽是10米.
(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).问:此船能否顺利通过这座拱桥?
如图9,边长为5的正方形 的顶点
的顶点 在坐标原点处,点
在坐标原点处,点 分别在
分别在 轴、
轴、 轴的正半轴上,点
轴的正半轴上,点 是
是 边上的点(不与点
边上的点(不与点 重合),
重合), ,且与正方形外角平分线
,且与正方形外角平分线 交于点
交于点 .
.
(1)当点 坐标为
坐标为 时,试证明
时,试证明 ;
;
(2)如果将上述条件“点 坐标为(3,0)”改为“点
坐标为(3,0)”改为“点 坐标为(
坐标为( ,0)(
,0)( )”,结论
)”,结论 是否仍然成立,请说明理由;
是否仍然成立,请说明理由;
(3)在 轴上是否存在点
轴上是否存在点 ,使得四边形
,使得四边形 是平行四边形?若存在,用
是平行四边形?若存在,用 表示点
表示点
的坐标;若不存在,说明理由.
已知二次函数 的图象经过
的图象经过 和
和 三点
三点
(1)若该函数图象顶点恰为点 ,写出此时
,写出此时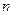 的值及
的值及 的最大值;
的最大值;
(2)当 时,确定这个二次函数的解析式,并判断此时
时,确定这个二次函数的解析式,并判断此时 是否有最大值;
是否有最大值;
(3)由(1)、(2)可知,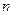 的取值变化,会影响该函数图象的开口方向.请你求出
的取值变化,会影响该函数图象的开口方向.请你求出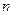 满足
满足
什么条件时, 有最小值?
有最小值?
2010年6月4日,乌鲁木齐市政府通报了首府2009年环境质量公报,其中空气质量级别分布统计图如图8所示,请根据统计图解答以下问题:
(1)写出2009年乌鲁木齐市全年三级轻度污染天数:
(2)求出空气质量为二级所对应扇形圆心角的度数(结果保留到个位);
(3)若到2012年,首府空气质量良好(二级及二级以上)的天数与全年天数(2012年是闰年,全年有366天)之比超过85%,求2012年空气质量良好的天数要比2009年至少增加多少天?