高中物理计算题

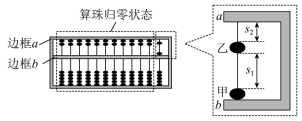
算盘是我国古老的计算工具，中心带孔的相同算珠可在算盘的固定导杆上滑动，使用前算珠需要归零，如图所示，水平放置的算盘中有甲、乙两颗算珠未在归零位置，甲靠边框b，甲、乙相隔 $s_1=3.5\times {10}^{-2}\text{m}$，乙与边框a相隔 $s_2=2.0\times {10}^{-2}\text{m}$，算珠与导杆间的动摩擦因数 $\mu =0.1$。现用手指将甲以 $0.4\text{m/s}$的初速度拨出，甲、乙碰撞后甲的速度大小为 $0.1\text{m/s}$，方向不变，碰撞时间极短且不计，重力加速度g取 $10{\text{m/s}}^2$。

（1）通过计算，判断乙算珠能否滑动到边框a；

（2）求甲算珠从拨出到停下所需的时间。

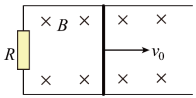
如图，间距为l的光滑平行金属导轨，水平放置在方向竖直向下的匀强磁场中，磁场的磁感应强度大小为B，导轨左端接有阻值为R的定值电阻，一质量为m的金属杆放在导轨上。金属杆在水平外力作用下以速度 $v_0$向右做匀速直线运动，此时金属杆内自由电子沿杆定向移动的速率为 $u_0$。设金属杆内做定向移动的自由电子总量保持不变，金属杆始终与导轨垂直且接触良好，除了电阻R以外不计其它电阻。

（1）求金属杆中的电流和水平外力的功率；

（2）某时刻撤去外力，经过一段时间，自由电子沿金属杆定向移动的速率变为 $\frac{u_0}{2}$，求：

（i）这段时间内电阻R上产生的焦耳热；

（ii）这段时间内一直在金属杆内的自由电子沿杆定向移动的距离。

如图，一长木板在光滑的水平面上以速度 $v_0$向右做匀速直线运动，将一小滑块无初速地轻放在木板最右端。已知滑块和木板的质量分别为m和2m，它们之间的动摩擦因数为μ，重力加速度为g。

（1）滑块相对木板静止时，求它们的共同速度大小；

（2）某时刻木板速度是滑块的2倍，求此时滑块到木板最右端的距离；

（3）若滑块轻放在木板最右端的同时，给木板施加一水平向右的外力，使得木板保持匀速直线运动，直到滑块相对木板静止，求此过程中滑块的运动时间以及外力所做的功。

一列沿x轴正方向传播的简谐横波，其波源的平衡位置在坐标原点，波源在 $0~4s$内的振动图像如图（a）所示，已知波的传播速度为 $0.5m/s$。

（1）求这列横波的波长；

（2）求波源在4s内通过的路程；

（3）在图（b）中画出 $t=4s$时刻的波形图。

如图，两水平面（虚线）之间的距离为 $H$ ，其间的区域存在方向水平向右的匀强电场。自该区域上方的A点将质量为 $m$ 、电荷量分别为 $q$ 和 $–q（q>0）$ 的带电小球M、N先后以相同的初速度沿平行于电场的方向射出。小球在重力作用下进入电场区域，并从该区域的下边界离开。已知N离开电场时的速度方向竖直向下；M在电场中做直线运动，刚离开电场时的动能为 $N$ 刚离开电场时动能的1.5倍。不计空气阻力，重力加速度大小为 g。求

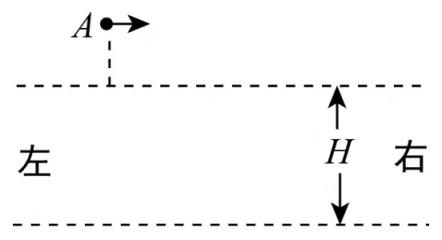
（1）M与N在电场中沿水平方向的位移之比；

（2）A点距电场上边界的高度；

（3）该电场的电场强度大小。

为提高冰球运动员的加速能力，教练员在冰面上与起跑线距离 $s_0$ 和 $s_1$ $（s_1<s_0）$ 处分别设置一个挡板和一面小旗，如图所示。训练时，让运动员和冰球都位于起跑线上，教练员将冰球以初速度 $v_0$ 击出，使冰球在冰面上沿垂直于起跑线的方向滑向挡板；冰球被击出的同时，运动员垂直于起跑线从静止出发滑向小旗。训练要求当冰球到达挡板时，运动员至少到达小旗处。假定运动员在滑行过程中做匀加速运动，冰球到达挡板时的速度为 $v_1$ 。重力加速度大小为 $g$ 。求

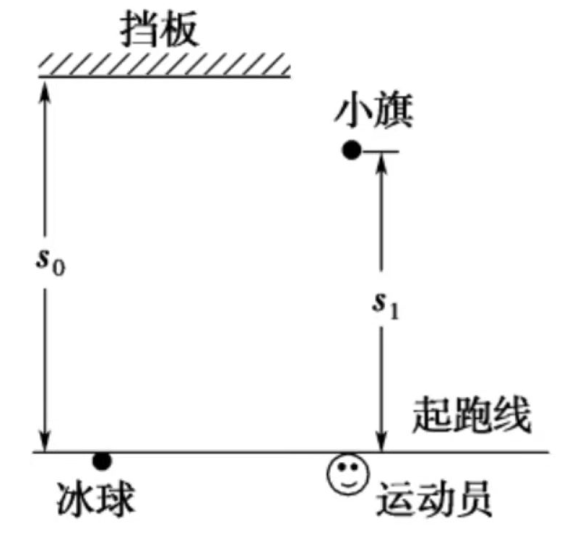
（1）冰球与冰面之间的动摩擦因数；

（2）满足训练要求的运动员的最小加速度。

如图，两个滑块 A和 B的质量分别为 $m_A=1\text{kg}$ 和 $m_B=5\text{kg}$ ，放在静止于水平地面上的木板的两端，两者与木板间的动摩擦因数均为 ${\mu }_1=0.5$ ；木板的质量为 $m=4\text{kg}$ ，与地面间的动摩擦因数为 ${\mu }_2=0.1$ 。某时刻 A、 B两滑块开始相向滑动，初速度大小均为 $v_0=3\text{m/s}$ 。 A、 B相遇时， A与木板恰好相对静止。设最大静摩擦力等于滑动摩擦力，取重力加速度大小 $g=10\text{m/}{\text{s}}^2$ 。求

（1） B与木板相对静止时，木板的速度；

（2） A、 B开始运动时，两者之间的距离。

静止在水平地面上的两小物块A、B，质量分别为m _A=l.0 kg，m _B=4.0 kg；两者之间有一被压缩的微型弹簧，A与其右侧的竖直墙壁距离l=1.0m，如图所示。某时刻，将压缩的微型弹簧释放，使A、B瞬间分离，两物块获得的动能之和为E _k=10.0 J。释放后，A沿着与墙壁垂直的方向向右运动。A、B与地面之间的动摩擦因数均为u=0.20。重力加速度取g=10 m/s²。A、B运动过程中所涉及的碰撞均为弹性碰撞且碰撞时间极短。

   

（1）求弹簧释放后瞬间A、B速度的大小；    

（2）物块A、B中的哪一个先停止？该物块刚停止时A与B之间的距离是多少？    

（3）A和B都停止后，A与B之间的距离是多少？    

空间存在一方向竖直向下的匀强电场，O、P是电场中的两点。从O点沿水平方向以不同速度先后发射两个质量均为m的小球A、B。A不带电，B的电荷量为 $\mathrm{q}\mathrm{（}\mathrm{q}>0\mathrm{）}$ 。A从O点发射时的速度大小为 ${\mathrm{v}}_0$ ， 到达P点所用时间为 $\mathrm{t}$ ；B从O点到达P点所用时间为 $\frac{t}{2}$ 。重力加速度为 $\mathrm{g}$ ，求   

（1）电场强度的大小；    

（2）B运动到P点时的动能。    

如图，两金属板P、Q水平放置，间距为d。两金属板正中间有一水平放置的金属网G，PQG的尺寸相同。G接地，PQ的电势均为 $\phi$ （ $\phi$ >0）。质量为m，电荷量为q（q>0）的粒子自G的左端上方距离G为h的位置，以速度v0平行于纸面水平射入电场，重力忽略不计。

（1）求粒子第一次穿过G时的动能，以及她从射入电场至此时在水平方向上的位移大小；    

（2）若粒子恰好从G的下方距离G也为h的位置离开电场，则金属板的长度最短应为多少？    

一足够长的条状区域内存在匀强电场和匀强磁场,其在 $\mathit{xOy}$ 平面内的截面如图所示：中间是磁场区域,其边界与y轴垂直,宽度为1,磁感应强度的大小为 $B$ ,方向垂真于 $\mathit{xOy}$ 平面:磁场的上下两侧为电场区域,宽度均为 $r$ ,电场强度的大小均为 $E$ ,方向均沿x轴正方向:M、N为条状区域边界上的两点,它们的连线与y轴平行。一带正电的粒子以某一速度从M点沿y轴正方向射入电场,经过一段时间后恰好以从M点入射的速度从N点沿y轴正方向射出。不计重力。

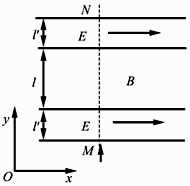
（1）定性画出该粒子在电磁场中运动的轨迹；    

（2）求该粒子从M点入射时速度的大小；    

（3）若该粒子进入磁场时的速度方向恰好与x轴正方向的夹角为 $\frac{x}{6}$ ,求该粒子的比荷及其从M点运动到N点的时间    

汽车 $A$ 在水平冰雪路面上行驶。驾驶员发现其正前方停有汽车 $B$ ,立即采取制动措施,但仍然撞上了汽车 $B$ .两车碰撞时和两车都完全停止后的位置如图所示,碰撞后 $B$ 车向前滑动了 $4.5m$ , $A$ 车向前滑动了 $2.0m$ ·已知 $A$ 和 $B$ 的质量分别为 $2.0x{1.0}^3\mathit{kg}$ 和 $1.5x{1.0}^3\mathit{kg}$ ·两车与该冰雪路面间的动摩擦因数均为0.10,两车碰撞时间极短,在碰撞后车轮均没有滚动,重力加速度大小 $g=10m/s^2$ ,求

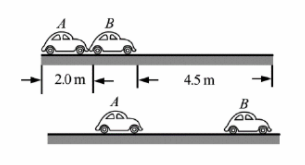
（1）碰撞后的瞬间 $B$ 车速度的大小    

（2）碰撞前的瞬间 $A$ 车速度的大小    

如图,在y>0的区域存在方向沿y轴负方向的匀强电场,场强大小为E，在y<0的区域存在方向垂直于xOy平面向外的匀强磁场。一个氕核 ¹ ₁H和一个氚核 ² ₁H先后从y轴上y=h点以相同的动能射出,速度方向沿x轴正方向。已知 ₁ ¹H进入磁场时,速度方向与x轴正方向的夹角为60°,并从坐标原点O处第一次射出磁场。 ₁ ¹H的质量为m,电荷量为q不计重力。求

（1） ₁ ¹H第一次进入磁场的位置到原点O的距离    

（2）磁场的磁感应强度大小    

（3） ₂ ¹H第一次离开磁场的位置到原点O的距离

一质量为 $8.00\times {10}^{4}4\mathit{kg}$的太空飞船从其飞行轨道返回地面．飞船在离地面高度 $1.60\times {10}^{5}m$处以7.5×10³ m/s的速度进入大气层，逐渐减慢至速度为 $100m/s$时下落到地面．取地面为重力势能零点，在飞船下落过程中，重力加速度可视为常量，大小取为 $9.8m/s^2$． （结果保留2位有效数字）

（1）分别求出该飞船着地前瞬间的机械能和它进入大气层时的机械能；

（2）求飞船从离地面高度 $600m$处至着地前瞬间的过程中克服阻力所做的功，已知飞船在该处的速度大小是其进入大气层时速度大小的 $2.0\%$．

如图，水平面（纸面）内间距为l的平行金属导轨间接一电阻，质量为m、长度为l的金属杆置于导轨上， $t=0$ 时，金属杆在水平向右、大小为F的恒定拉力作用下由静止开始运动，t ₀时刻，金属杆进入磁感应强度大小为B、方向垂直于纸面向里的匀强磁场区域，且在磁场中恰好能保持匀速运动．杆与导轨的电阻均忽略不计，两者始终保持垂直且接触良好，两者之间的动摩擦因数为μ．重力加速度大小为g．求：

①金属杆在磁场中运动时产生的电动势的大小；

②电阻的阻值．