高中物理电磁场综合题

(1996年全国，26)设在地面上方的真空室内，存在匀强电场和匀强磁场，已知电场强度和磁感应强度的方向是相同的，电场强度的大小为E＝4.0V/m，磁感应强度的大小B＝0.15T，今有一带负电的质点以v＝20m/s的速度在此区域内沿垂直场强方向做匀速直线运动，求此带电质点的电量与质量之比q/m以及磁场的所有可能方向(角度可用反三角函数表示)．

如图11-2-15所示，在倾角为30⁰的斜面上，放置两条宽L=0.5m的平行导轨，将电源、滑动变阻器用导线连接在导轨上，在导轨上横放一根质量m=0.2kg的金属杆ab，电源电动势E=12V，内阻r=0．3Ω，金属杆与导轨间最大静摩擦力为fm=0.6N，磁场方向垂直轨道所在平面，B=0.8T．金属杆ab的电阻为0.2Ω，导轨电阻不计．欲使杆的轨道上保持静止，滑动变阻器的使用电阻的范围多大?(g取10m／s²)

如图16－107所示，两个共轴的圆筒形金属电极，外电极接地，其上均匀分布着平行于轴线的四条狭缝a、b、c和d，外筒的外半径为r0．在圆筒之外的足够大区域中有平行于轴线方向的均匀磁强，磁感应强度的大小为B．在两极间加上电压，使两圆筒之间的区域内有沿半径向外的电场．一质量为m、带电量为＋q的粒子，从紧靠内筒且正对狭缝a的S点出发，初速为零．如果该粒子经过一段时间的运动之后恰好又回到出发点S，则两电极之间的电压U应是多少？(不计重力，整个装置在真空中)．

某空间存在着变化的电场和另一变化的磁场，电场方向向右，即图中由b点到c点的方向，电场强度大小变化如图中E-t图像，磁感强度变化如图中B-t图像。已知ab垂直于bc，，在a点，从第1s末时刻开始，每隔2s有一相同带电粒子（粒子重力不计）沿ab方向以速度v射出，这些粒

子都恰能击中c点，且粒子在ac间运动时间小于1s，求：
(1)图像中E₀和B₀的比值。
(2)第二个粒子和第一个粒子从射出到击中c点所用时间的比值。

如图所示，PQ为一块长为L，水平放置的绝缘平板，整个空间存在着由右向左的匀强电场，板的右半部分还存在着垂直纸面向里的有界匀强磁场。一质量为m带电量为q的物体，从板左端P由静止开始做匀加速运动，进入磁场后作匀速运动.离开磁场后又做匀减速速运动,最后停在C点。已，物体与绝缘板间摩擦因数为.
求：(1)物体带何种电？
(2)物体与板碰撞前后的速度各是多大？
(3)电场强度E及磁感强度B多大？

如图中，XOZ是光滑水平面；空间有沿+Z方向的匀强磁场，其磁感强度为B。现有两块平行金属板，彼此间距为d，构成一个电容为C的平行板电容器；在两板之间焊一根垂直两板的金属杆PP'，已知两板和杆PP'的总质量为m，若对此杆PP'作用一个沿+X方向的恒力F，试推求此装置匀加速平移的加速度a的表达式。（用B、c、d、m、F等表示）

长方形导体如图放置，在垂直x轴的两面加电压U，电流为I且沿x轴正方向流动．如沿Z轴正方向加一个磁感强度为B的匀强磁场，则在垂直于y轴的两个侧面上得到电压为U'．试求导体中单位体积内的自由电子数n．

如图所示，很长的平行边界面M、N、P间距分别为，其间分别有磁感强度为B1与的匀强磁场区I和II，磁场方向均垂直纸面向里。已知≠，一个带正电的粒子电量为q，质量为m，以大小为v_o的速度垂直边界面M与磁场方向射入MN间磁场区，试讨论粒子速度v_o应满足什么条件，才可通过这两个磁场区，并从边界面P射出？（不计粒子重力）

如图所示，一块长为b，宽为a，厚为h=0.1mm的铜片，放在B=1.5T的匀强磁场中，磁场方向与铜片表面垂直．若铜片中通有自左向右的I=2A的电流时，铜片前后两侧面会形成一个电势差．金属导线中电流I与自由电子定向移动速度v、导线横截面积S间存在关系I=neSv，式中n为单位体积内的自由电子个数，若每个金属导体中每个原子仅提供一个自由电子(即自由电子数与金属内所含原子数相同)，试求：

(1)铜片前后侧面哪一面电势高?电势差为多少?
(2)在磁场和电流不变的条件下，如何改变金属片尺寸，可以增大该电势差?
(铜的密度近似为9.0×，铜的原子量近似为60，阿伏伽德罗常数为6.0×，电子电量为1.6×C)

如图16－103(所示，在x轴上方有匀强电场，场强为E，在x轴下方有匀强磁场，磁感应强度为B，方向如图所示，在x轴上有一点M，离O点距离为L，现有一带电量为＋q的粒子，从静止开始释放后能经过M点，求：
(1)如果此粒子放在y轴上，其坐标应满足什么关系？
(2)如果此粒子不放在y轴上，其x、y坐标应满足什么关系？(重力忽略不计)

如图16－101所示，电源电动势E＝2V，r＝0.5Ω，竖直导轨宽L＝0.2m，导轨电阻不计．另有一金属棒质量m＝0.1kg、电阻R＝0.5Ω，它与导轨间的动摩擦因数μ＝0.4，靠在导轨的外面．为使金属棒不滑，施一与纸面夹角为30°且与导体棒垂直指向纸里的匀强磁场，(设最大静摩擦力等于滑动摩擦力，取g＝10m/s2)．求：
(1)此磁场的方向．
(2)磁感强度B的取值范围．

如图16－109所示，厚度为h，宽度为d的导体板放在垂直于它的磁感强度为B的均匀磁场中，当电流通过导体板时，在导体板的上侧面A和下侧面A′之间会产生电势差，这种现象称为霍尔效应，实验表明，当磁场不太强时，电势差U、电流I和B的关系为U＝K·IB/d，式中的比例系数K称为霍尔系数．霍尔效应可解释如下：外部磁场的洛仑兹力使运动的电子聚集在导体板的一侧，在导体板的另一侧出现多余的正电荷，从而形成横向电场．横向电场对电子施加与洛仑兹力方向相反的静电力，当静电力与洛仑兹力达到平衡时，导体板上下两侧之间就会形成稳定的电势差．设电流I是电子的定向流动形成的，电子的平均定向速度为v，电量为e，回答下列问题：
(1)达到稳定状态时，导体板上侧面A的电势________下侧面A′的电势(填高于、低于或等于)．
(2)电子所受洛仑兹力的大小为________．
(3)当导体板上下两侧之间的电势差为U时，电子所受静电力的大小为________．
(4)由静电力和洛仑兹力平衡的条件，证明霍尔系数为K＝1/ne，其中n代表导体板单位体积中电子的个数．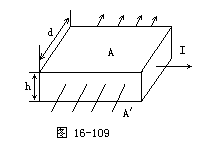

如图所示是利用“霍尔元件”测量磁场的磁感应强度的示意图．“霍尔元件”是由半导体材料制成的矩形薄片，它的四边各有一条引线．把它放入匀强磁场中，使薄片平面与磁场方向垂直，A．B两引线与直流电源相连，C．D两引线与电压表相连．已知该半导体材料中单位体积内的自由电荷数为n、每个自由电荷的电量为q，元件的A．B两边距离为A．C．D两边距离为B．厚度为d，通过电流表读出元件中通过的电流为I、从电压表读出电压为U．

(1)已知磁场方向向下，C．D两引线哪边的电势较高？
(2)求磁感应强度B的大小．
 

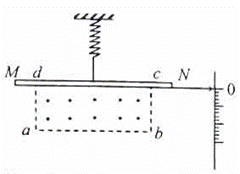
图为一电流表的原理示意图。质量为的均质细金属棒的中点处通过一绝缘挂钩与一竖直悬挂的弹簧相连，弹簧劲度系数为。在矩形区域内有匀强磁场，磁感应强度大小为B，方向垂直纸面向外。与的右端连接的一绝缘轻指针可指示标尺上的读数，的长度大于。当中没有电流通过且处于平衡状态时，与矩形区域的边重合：当中有电流通过时，指针示数可表示电流强度。
（1）当电流表示数为零时，弹簧伸长多少？（重力加速度为）
（2）若要电流表正常工作，的哪一端应与电源正极相接？
（3）若=2.0N/m，=0.20m，=0.050m，=0.20T，此电流表的量程是多少？（不计通电时电流产生的磁场的作用）
（4）若将量程扩大2倍，磁感应强度应变为多大？