神舟七号载人航天飞行获得了圆满成功，我国航天员首次成功实施空间出舱活动、飞船首次成功实施释放小伴星的实验，实现了我国空间技术发展的重大跨越．已知飞船在地球上空的圆轨道上运行时离地面的高度为h．地球半径为R，地球表面的重力加速度为g．求飞船在该圆轨道上运行时：
（1）速度v的大小和周期T．
（2）速度v与第一宇宙速度的比值．
我国神舟九号飞船已于2012年6月16日成功发射，与“天官一号”目标飞行器展开手控交会对接，飞行乘组由3名航天员组成。天宫一号目标飞行器，是我国自主研制的全新的载人飞行器，计划在轨道上的工作运行时间为2年，它可以与载人飞船进行多次对接。已知“天宫一号”飞行器质量为m，运行高度为h，地球半径为R，地球表面的重力加速度为g。求：
（1）天宫一号受到地球的万有引力大小；
（2）天宫一号的运行周期。
已知某行星的半径为R，行星表面重力加速度为g，不考虑行星自转的影响。若有一卫星绕该行星做匀速圆周运动，运行轨道距行星表面高度为h，求卫星的运行周期T。
我国首个月球探测计划“嫦娥工程”将分三个阶段实施，大约用十年左右时间完成，这极大地提高了同学们对月球的关注程度．以下是某同学就有关月球的知识设计的问题，请你解答：若已知地球半径为
，地球表面的重力加速度为
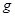，月球绕地球运动的周期为
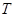，且把月球绕地球的运动近似看做是匀速圆周运动。试求出月球绕地球运动的轨道半径
。
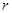如图所示，A是地球的同步卫星，另一卫星B的圆形轨道位于赤道平面内，离地面高度为h，已知地球半径为R，地球自转角速度为
，地球表面的重力加速度为g，O为地球中心．
（1）求卫星B的运行周期；
（2）如果卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近（O、B、A在同一直线上），则至少经过多长时间，它们再一次相距最近？
从地球表面向火星发射火星探测器。设地球和火星都在同一平面上绕太阳做匀速圆周运动。火星轨道半径
为地球轨道半径
的1.5倍。简单而又比较节省能量的发射过程可分为两步进行：第一步，在地球表面用火箭对探测器进行加速，使之获得足够的动能，成为一个绕地球运行的人造卫星；第二步，在适当时刻点燃与探测器连在一起的火箭发动机。在短时间内对探测器沿原方向加速，使其速度数值增加到适当值，使探测器沿半个椭圆轨道（该椭圆长轴两端分别与地球公转轨道及火星公转轨道相切）射到火星上。如图(a)所示。已知地球半径
，重力加速度g=10m/s2。
（1）为使探测器成为绕地球运行的人造卫星，探测器在地面附近至少要获得多大的速度(不考虑地球自转)。
（2）求火星探测器的飞行时间为多少天（已知
，1年为365天）。
（3）当探测器绕地球运行稳定后，在某年 3月 1 日零时测得探测器与火星之间的角度为 60°，如图(b)所示。求应在何年何月何日点燃探测器上的火箭发动机方能使探测器恰好落在火星表面(时间计算仅需精确到天，已知
，1年为365天)。
a、b两颗卫星在同一轨道平面内绕地球作匀速圆周运动，地球半径为R，a 卫星离地面高度为R，b卫星离地面高度为3R，则a、b两卫星周期之比为多大？若某时刻两卫星正好同时通过地面上同一点的正上方，a卫星至少经过多少个周期两卫星相距最远？
如图，P、Q为某地区水平地面上的两点，在P点正下方一球形区域内储藏有石油，假定区域周围岩石均匀分布，密度为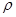
；石油密度远小于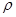，可将上述球形区域视为空腔。如果没有这一空腔，则该地区重力加速度（正常值）沿竖直方向；当存在空腔时，该地区重力加速度的大小和方向会与正常情况有微小偏高。重力加速度在原坚直方向（即PO方向）上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量，常利用P点附近重力加速度反常现象。已知引力常数为G。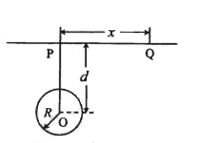
（1）设球形空腔体积为V，球心深度为d（远小于地球半径），
=x，求空腔所引起的Q点处的重力加速度反常
（2）若在水平地面上半径L的范围内发现：重力加速度反常值在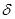
与
（k>1）之间变化，且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的，试求此球形空腔球心的深度和空腔的体积。
在某未知星球表面距地面6m的高度将一物体以水平速度15m/s抛出，落地时水平位移为30m
（1）求此星球表面的重力加速度
（2）若此星球的半径为5000km，求此星球的质量（保留一位有效数字）（G=6.67×10-11N·m2/kg2）
为了实现登月计划，先要测算地月之间的距离。已知地球表面重力加速度为g，地球半径为R，在地面附近物体受到地球的万有引力近似等于物体在地面上的重力，又知月球绕地球运动的周期为T，万有引力常量为G。则：
（1）地球的质量为多少？（2）地月之间的距离约为多少？
已知地球半径为R，地球表面重力加速度为g，不考虑地球自转的影响。
（1）推导第一宇宙速度v1的表达式；
（2）若卫星绕地球做匀速圆周运动，运行轨道距离地面高度为h，求卫星的运行周期T。
如图所示，离质量为M、半径为R、密度均匀的球体表面R远处有一质量为m的质点，此时M对m的万有引力为F1 ；当从M中挖去一半径为r＝
R的球体时，剩下部分对m的万有引力为F2.则F1与F2之比是多少？
）
kg，但是它的半径才不过10km，求：（1）此中子星表面的自由落体加速度。
N
）
粤公网安备 44130202000953号