高中物理万有引力定律及其应用计算题

已知万有引力常量为G，地球半径为R，同步卫星距地面的高度为h，地球的自转周期为T。某同学根据以上条件，提出一种计算地球赤道表面的物体随地球自转的线速度大小的方法：地球赤道表面的物体随地球作匀速圆周运动，由牛顿运动定律有。又根据地球上的物体的重力与万有引力的关系，可以求得地球赤道表面的物体随地球自转的线速度的大小v。
（1）请判断上面的方法是否正确。如果正确，求出v的结果；如不正确，给出正确的解法和结果。
（2）由题目给出的条件再估算地球的质量。

一物体在地球表面重90N，它在以a=g/3的加速度(g为地球表面上重力加速度)加速上升的火箭中的视重为40N，则此火箭离地球表面的距离为地球半径的多少倍?

“嫦娥一号”探月卫星在空中运动的简化示意图如图所示。卫星由地面发射后，经过发射轨道进入停泊轨道，在停泊轨道经过调速后进入地月转移轨道，再次调速后进入工作轨道。已知卫星在工作轨道上运行的半径为R，月球半径为r，地球表面重力加速度为g，月球表面重力加速度是地球表面重力加速度的1/6，求卫星在工作轨道上运行的周期。

在福建省科技馆中，有一个模拟万有引力的装置。在如图1所示的类似锥形漏斗固定的容器中，有两个小球在该容器表面上绕漏斗中心轴做水平圆周运动，其运行能形象地模拟了太阳系中星球围绕太阳的运行。图2为示意图，图3为其模拟的太阳系运行图。图2中离中心轴的距离相当于行星离太阳的距离。
（1）在图3中，设行星A₁和B₂离太阳距离分别为r₁和r₂，求A₁和B₂运行速度大小之比。
（2）在图2中，若质量为m的A球速度大小为v，在距离中心轴为x₁的轨道面上旋转，由于受到微小的摩擦阻力，A球绕轴旋转同时缓慢落向漏斗中心。当其运动到距离中心轴为x₂的轨道面时，两轨道面之间的高度差为H。求此过程中A球克服摩擦阻力所做的功。

某颗人造地球卫星在距地面高度为h的圆形轨道上绕地球飞行，其运动可视为匀速圆周运动。已知地球半径为R，地面附近的重力加速度为g。求卫星在圆形轨道上运行速度的表达式和运行周期的表达式。

已知某行星的半径为R，以其第一宇宙速度运行的卫星绕行星运行的周期为T，该行星的同步卫星的运行速度为v，求：（1）该行星的同步卫星距行星表面的高度h。（2）该行星的自转周期T＇。

我国发射的“嫦娥一号”探月卫星沿近似于圆形的轨道绕月飞行.为了获得月球表面全貌的信息,让卫星轨道平面缓慢变化.卫星将获得的信息持续用微波信号发回地球.设地球和月球的质量分别为M和m,地球和月球的半径分别为R和R₁,月球绕地球的轨道半径和卫星绕月球的轨道半径分别为r和r₁,月球绕地球转动的周期为T.假定在卫星绕月运行一个周期内卫星轨道平面与地月连心线共面.求在该周期内卫星发射的微波信号因月球遮挡而不能到达地球的时间(有M､m､R､R₁､r､r₁和T表示,忽略月球绕地球转动对遮挡时间的影响).

某宇航员在飞船发射前测得自身连同宇航服等随身装备共重840 N,在火箭发射阶段,发现当飞船随火箭以a=g/2的加速度匀加速竖直上升到某位置时(其中g为地球表面处的重力加速度),其身下体重测试仪的示数为1220 N.设地球半径R="6400" km,地球表面重力加速度g="10" m/s²(求解过程中可能用到 ="1.03," 1.02).问:
(1)该位置处的重力加速度g′是地面处重力加速度g的多少倍?
(2)该位置距地球表面的高度h为多大?

天文学家将相距较近､仅在彼此的引力作用下运行的两颗恒星称为双星.双星系统在银河系中很普遍.利用双星系统中两颗恒星的运动特征可计算出它们的总质量.已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,周期均为T,两颗恒星之间的距离为r,试推算这个双星系统的总质量.(引力常量为G)

宇航员站在一星球表面上的某高处，沿水平方向抛出一个小球，经过时间t，小球落到星球表面，测得抛出点与落地点之间的距离为L。若抛出时的初速增大到2倍，则抛出点与落地点之间的距离为L。已知两落地点在同一水平面上，该星球的半径为R，万有引力常数为G。
（1）求该星球的质量M
（2）求在距离该星球表面H高处的轨道上做匀速圆周运动的飞行器的运动周期。

已知火星半径R_火=R_地，火星质量M_火=M_地，问：
（1）火星表面处的重力加速度与地球表面处的重力加速度之比为多少？
（2）若想在火星上发射一颗接近火星表面运行的人造卫星，则发射速度与在地球上发射一颗近地卫星的发射速度之比为多少？

一颗在赤道上空运行的人造卫星，其轨道半径为（R为地球半径），卫星的运动方向与地球自传方向相同。已知地球自传的角度为，地球表面处的重力加速度为g
（1）求人造卫星绕地球转动的角速度
（2）若某时刻卫星通过赤道上某建筑物的正上方，求它下次通过该建筑物上方需要的时间

“神舟九号”飞船与“天宫一号”目标飞行器在2012年6月18日14时07分实现自动交会对接，形成组合体。并于6月24日12时55分第一次实现了手动交会对接，使我国载人航天空间交会实验获得重大成功。

（1）如图所示，为“神舟九号”的示意图，P₁、P₂、P₃、P₄是四个喷气发动机，每台发动机开动时都能向“神舟九号”提供动力，但不会使其转动。当“神舟九号”与“天宫一号”在同一轨道运行，相距30m停泊（相对静止）时，若仅开动发动机P₁使“神舟九号”瞬间获得大于“天宫一号”的运行速度，则它们能否实现交会对接？（ 只答“能”或“不能” ）
（2）若地球表面的重力加速度为g，地球半径为R，组合体运行的圆轨道距地面的高度为h，那么，组合体绕地球运行的周期是多少？

一颗人造地球卫星绕地球做匀速圆周运动，卫星离地面的高度为h。已知地球半径为R，地面重力加速度为g。求：
（1）卫星的线速度；
（2）卫星的周期。

为了迎接太空时代的到来，美国国会通过一项计划：在2050年前建造成太空升降机，就是把长绳的一端搁置在地球的卫星上，另一端系住长降机。放开绳，升降机能到达地球上；人坐在升降机里，在卫星上通过电动机把升降机拉到卫星上。已知地球表面的重力加速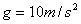，地球半径为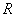。求：
（1）某人在地球表面用体重计称得重180N，站在升降机中，当升降机以加速度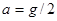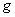（为地球表面处的重力加速度）竖直上升时，在某处此人再一次用同一体重计称得视重为170N，忽略地球自转的影响，求升降机此时距地面的高度；
（2）如果把绳的一端搁置在同步卫星上，地球自转的周期为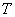，求绳的长度至少为多长。