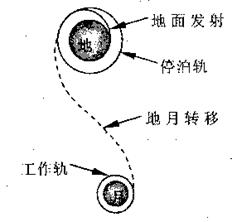
“嫦娥一号”探月卫星在空中运动的简化示意图如图所示。卫星由地面发射后，经过发射轨道进入停泊轨道，在停泊轨道经过调速后进入地月转移轨道，再次调速后进入工作轨道。已知卫星在工作轨道上运行的半径为R，月球半径为r，地球表面重力加速度为g，月球表面重力加速度是地球表面重力加速度的1/6，求卫星在工作轨道上运行的周期。