一艘宇宙飞船飞近某一新发现的行星，并进入靠近该行星表面的圆形轨道绕行数圈后，着陆在该行星上。飞船上备有以下实验器材：①精确秒表一只；②已知质量为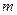
的物体一个；③弹簧测力计一个。若宇航员在绕行时测出了飞船绕行星运行的周期为T，着陆后质量为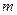的物体所受重力为F。并已知万有引力常量为G，行星的自转可忽略不计，试求出该星球的半径R及星球的质量M。
某星球质量是地球质量的五分之一，该星球的半径是地球半径的两倍.在该星球表面以16m/s的速度竖直上抛一质量为60kg的物体.求物体上升的最大高度是多少? （g=10m/s2）
为了实现登月计划，先要测算地月之间的距离。已知地球表面重力加速度为g，地球半径为R，在地面附近物体受到地球的万有引力近似等于物体在地面上的重力，又知月球绕地球运动的周期为T，万有引力常量为G。则：
（1）地球的质量为多少？
（2）地月之间的距离约为多少？
某宇航员在飞船发射前测得自身连同宇航服等随身装备共重840 N,在火箭发射阶段,发现当飞船随火箭以a=g/2的加速度匀加速竖直上升到某位置时(其中g为地球表面处的重力加速度),其身下体重测试仪的示数为1220 N.设地球半径R="6400" km,地球表面重力加速度g="10" m/s2(求解过程中可能用到
=1.03，
1.02).问:
(1)该位置处的重力加速度g′是地面处重力加速度g的多少倍?
(2)该位置距地球表面的高度h为多大?
宇宙中存在一些离其他恒星较远的、由质量相等的三颗星组成的三星系统，通常可忽略其他星体对它们的引力作用。现已观测到稳定的三星系统存在两种基本的构成形式：一种是三颗星位于同一直线上，两颗星围绕中央星在同一半径为R的圆轨道上运行；另一种形式是三颗星位于等边三角形的三个顶点上，并沿外接于等边三角形的圆轨道上运行。设每个星体的质量均为m。万有引力常量为G。
（1）试求第一种形式下，星体运动的线速度和周期；
（2）假设两种形式星体的运动周期相同，第二种形式下星体之间的距离应为多少？
已知地球的半径为R，地球表面的重力加速度大小为g，万有引力常量为G，不考虑地球自转的影响．试求：
（1）卫星环绕地球运行的第一宇宙速度
的大小；
（2）若卫星绕地球做匀速圆周运动且运行周期为T，求卫星运行的轨道半径r；
（3）由题干所给条件，推导出地球平均密度
的表达式．
天文工作者观测到某行星的半径为
r0，自转周期为T0，它有一颗卫星，轨道半径为r，绕行星公转周期为T。求：
（1）该行星表面的重力加速度g为多大？
（2）要在此行星的赤道上发射一颗同步人造卫星，使其轨道在赤道上方，则该同步卫星离地表的高度h为多大？
一宇航员抵达一半径为Ｒ的星球表面后，为了测定该星球的质量Ｍ，做如下实验，取一根细线穿过光滑的细直管，细线一端栓一质量为m的砝码，另一端连在一固定的测力计上，手握细直管抡动砝码，使它在竖直平面内做完整的圆周运动。停止抡动细直管，砝码可继续在同一竖直平面做完整的圆周运动。如图所示，观察测力计得到，当砝码运动到圆周的最低点时，测力计的读数为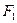
；当砝码运动到圆周的最高点时，测力计的读数为
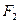。已知引力常量为Ｇ，试根据题中提供的条件和测量结果，求：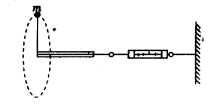
（1）该星球表面的重力加速度；
（2）该星球的质量Ｍ；
（3）该星球的第一宇宙速度。
已知地球质量为M，万有引力常量为G，现有一质量为m的卫星绕地球做匀速圆周运动，其轨道半径为r，求：
⑴卫星的线速度大小.
⑵卫星在轨道上做匀速圆周运动的周期
宇航员到达某行星表面后，用长为
的细线拴一小球，让球在竖直面内做圆周运动。他测得当球通过最高点的速度为
时，绳
中张力刚好为零。设行星的半径为R、引力常量为G，求：
（1）该行星表面的重力加速度大小
（2）该行星的质量
（3）在该行星表面发射卫星所需要的最小速度
月球自转一周的时间与月球绕地球运行一周的时间相等，都为T0。“
嫦娥1号”探月卫星于2007年11月7日成功进入绕月运行的“极月圆轨道”，这一圆形轨道通过月球两极上空，距月面的高度为h。若月球质量为M，月球半径为R，万有引力恒量为G。求：
（1）“嫦娥1号”绕月运行的周期。
（2）在月球自转一周的过程中，“嫦娥1号”将绕月运行多少圈？
已知地球半径为R，地球表面重力加速度为g，不考虑地球自转的影响。试推导第一宇宙速度v的表达式。
高空遥感探测卫星在距地球表面高为h处绕地球转动，如果地球质量为M，地球半径为R，人造卫星质量为m，万有引力常量为G，求：
（1）人造卫星的角速度多大？
（2）人造卫星绕地球转动的周期是多少？
（3）人造卫星的向心加速度多大？
某星球的半径是地球半径的2倍，质量为地球质量的8倍，则该星球表面的重力加速度约为多少？（地球表面重力加速度取
）
，计算在距地面高为h
=3600km的圆形轨道上的卫星做匀速圆周运动的线速度v和周期T。(结果保留两位有效数字)
粤公网安备 44130202000953号