高中物理万有引力定律及其应用计算题

质量为m的卫星发射前静止在地球赤道表面。假设地球可视为质量均匀分布的球体，半径为R。
（1）已知地球质量为M，自转周期为T，引力常量为G。求此时卫星对地表的压力N的大小；
（2）卫星发射后先在近地轨道上运行（轨道离地面的高度可以忽略不计），运行的速度大小为v₁，之后经过变轨成为地球的同步卫星，此时离地面高度为H，运行的速度大小为v₂。
a．求比值；
b．若卫星发射前随地球一起自转的速度大小为v₀，通过分析比较v₀、 v₁、v₂三者的大小关系。

2012年6月16日，“神舟九号”宇宙飞船搭载3名航天员飞天，并于6月18日14∶00与“天宫一号”成功对接。在发射时，“神舟九号”宇宙飞船首先要发射到离地面很近的圆轨道，然后经过多次变轨后，最终与在距地面高度为h的圆形轨道上绕地球飞行的“天宫一号”完成对接，之后，整体保持在距地面高度仍为h的圆形轨道上绕地球继续运行．已知地球半径为R，地面附近的重力加速度为g。求：
（1）地球的第一宇宙速度；
（2）“神舟九号”宇宙飞船在近地圆轨道运行的速度与对接后整体的运行速度之比。

据每日邮报2014年4月18日报道，美国国家航空航天局目前宣布首次在太阳系外发现“类地”行星。假如宇航员乘坐宇宙飞船到达该行星，进行科学观测：该行星自转周期为 T，宇航员在该行星“北极”距该行星地面附近H处自由释放—个小球（引力视为恒力），落地时间为t. 已知该行星半径为r，万有引力常量为G，求：
（1）该行星的第一宇宙速度；
（2）该行星的平均密度。

如图所示一宇航员站在一星球表面，用一根细绳一端固定在O点，另一端固定质量为m的小球，在最低点给小球某一速度让小球在竖直平面内做完整圆周运动，小球运动到最低点和最高点绳的拉力差为F，已知该星球的半径为R，万有引力常量为G。求该星球的质量M。

嫦娥三号将于今年12月发射，嫦娥三号及其月球车实现一系列重大突破，将完成在月球表面软着陆和巡视探测，实现中华民族五千年来九天揽月的梦想．一位勤于思考的同学为探月机械人设计了如下实验：在月球表面以初速度v₀竖直上抛出一个物体，测得物体的经过t时间落回．通过查阅资料知道月球的半径为R，引力常量为G，若物体只受月球引力的作用，上抛高度很小．求：
（1）月球的质量
（2）嫦娥三号在距月球表面高R处绕月球圆周运行的速率．

(10分)在天体运动中，把两颗相距较近的恒星称为双星，已知A、B两恒星质量分别为m₁和m₂，两恒星相距为L，两恒星分别绕共同的圆心做圆周运动，如图所示，求两恒星的轨道半径和角速度？（已知万有引力常量为G）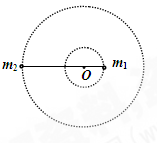

物体在地球表面重16 N，它在以5 m/s²的加速度加速上升的火箭中的视重为9 N，则此火箭离地球表面的距离为地球半径的多少倍？（设地球表面处g₀取10 m/s²）

已知引力常量G，地球半径R，月球和地球之间的距离r，同步卫星距地面的高度h，月球绕地球的运转周期T₁，地球的自转周期T₂，地球表面的重力加速度g，某同学根据以上条件，提出一种估算地球质量M的方法：同步卫星绕地心做圆周运动，由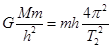得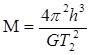
（1）请判断上面的结果是否正确，并说明理由，如不正确，请给出正确的解法和结果；
（2）请根据已知条件再提出两种估算地球质量的方法并解得结果（用上面所给的已知量表示）。

某星球的质量约为地球质量的8倍，半径约为地球半径的2倍。已知地球的第一宇宙速度为7.9 km/s，则航天器在该星球表面附近绕星球做匀速圆周运动的速度大小约为多少？

经过用天文望远镜长期观测，人们在宇宙中已经发现了许多双星系统，通过对它们的研究，使我们对宇宙中物质的存在形式和分布情况有了较深刻的认识，双星系统由两个星体组成，其中每个星体的线度都远小于两星体之间的距离，一般双星系统距离其他星体很远，可以当做孤立系统来处理。现根据对某一双星系统的光度学测量确定，该双星系统中每个星体的质量都是M，两者相距L，它们正围绕两者连线的中点做圆周运动。试求：
（1）该双星系统的运动周期；
（2）若该实验中观测到的运动周期为T_观测，且。为了理解T_观测 与T_计算的不同，目前有一种流行的理论认为，在宇宙中可能存在一种望远镜观测不到的暗物质。作为一种简化模型，我们假定在以这两个星体连线为直径的球体内均匀分布这种暗物质。若不考虑其他暗物质的影响，根据这一模型和上述观测结果确定该星系间这种暗物质的密度。

我国“神舟”五号飞船于2003年l0月15日在酒泉航天发射场由长征二号F运载火箭成功发射升空，若长征二号F运载火箭和飞船起飞时总质量为1.0×10⁵kg，起飞推动力为3.0×10⁶N，运载火箭发射塔高160m，试问：（g=10m/s²）
（1）运载火箭起飞时的加速度为多大？
（2）假如运载火箭起飞时推动力不变，忽略一切阻力和运载火箭质量的变化，试确定运载火箭需经多长时间才能飞离发射塔？
（3）这段时间内飞船中的宇航员承受了多大的压力？（设宇航员的质量为65kg）

在半径R＝5000 km 的某星球表面，宇航员做了如下实验．实验装置如图甲所示，竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成，将质量m＝0.2 kg 的小球从轨道AB上高H处的某点静止滑下，用力传感器测出小球经过C点时对轨道的压力F，改变H的大小，可测出相应的F大小，F随H的变化关系如图乙所示．求：

（1）圆轨道的半径．
（2）该星球的第一宇宙速度．

如图所示，A是地球的同步卫星．另一卫星B的圆形轨道位于赤道平面内，离地面高度为h.已知地球半径为R，地球自转角速度为ω0，地球表面的重力加速度为g，O为地球中心．

(1)求卫星B的运行周期．
(2)如卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近(O、B、A在同一直线上)，则至少经过多长时间，它们还能相距最近？

一个质量为1500 kg行星探测器从某行星表面竖直升空，发射时发动机推力恒定，发射升空后8 s末，发动机突然间发生故障而关闭；如图所示为探测器从发射到落回出发点全过程的速度图象；已知该行星表面没有大气，不考虑探测器总质量的变化；求：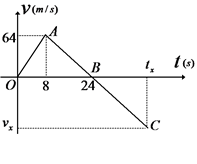

（1）探测器在行星表面上升达到的最大高度；
（2）探测器落回出发点时的速度；
（3）探测器发动机正常工作时的推力。

我国自主研制的北斗卫星导航系统包括5颗静止轨道卫星（同步卫星）和30颗非静止轨道卫星，将为全球用户提供高精度、高可靠性的定位、导航服务。
A为地球同步卫星，质量为m₁；B为绕地球做圆周运动的非静止轨道卫星，质量为m₂，离地面高度为h.已知地球半径为R，地球自转周期为T₀，地球表面的重力加速度为g。 求：
(1)卫星A运行的角速度；(2)卫星B运行的线速度。