高中物理万有引力定律及其应用计算题

如图所示，A是地球的同步卫星，另一卫星B的圆形轨道位于赤道平面内，离地面高度为h，已知地球半径为R，地球自转角速度为ω₀，地球表面的重力加速度为g，O为地球中心。求：

（1）卫星B的运行周期；
（2）若卫星B绕行方向与地球自转方向相同，某时刻A、B两 卫星相距最近（O、B、A在同一直线上），则至少经过多长时间，他们再一次相距最近？

由于地球自转的影响，地球表面的重力加速度会随纬度的变化而有所不同：若地球表面两极处的重力加速度大小为g₀，在赤道处的重力加速度大小为g，地球自转的周期为r，引力常量为G，地球可视为质量均匀分布的球体．求：
（1）地球半径R；
（2）地球的平均密度；
（3）若地球自转速度加快，当赤道上的物体恰好能“飘”起来时，求地球自转周期T'．

我国的“探月工程”计划将在2017年宇航员登上月球.若宇航员登上月球后，以初速度v₀竖直向上拋出一小球，测出小球从抛出到落回原处所需的     时间为t 。已知万有引力常量为G、月球的半径为 R ，不考虑月球自转的影响，求：
（1）求月球表面的重力加速度大小；
（2）月球的质量M ；
（3）飞船贴近月球表面绕月球做匀速圆周运动的周期T 。

2003年10月15日，我国神舟五号载人飞船成功发射.标志着我国的航天事业发展到了一个很高的水平.飞船在绕地球飞行的第5圈进行变轨，由原来的椭圆轨道变为距地面高度为h的圆形轨道.已知地球半径为R，地面处的重力加速度为g，引力常量为G,求：
⑴地球的质量；  ⑵飞船在上述圆形轨道上运行的周期T.

某一行星有一质量为m的卫星，以半径r，周期T做匀速圆周运动，行星的半径是R，万有引力常量为G，求：
（1）行星的质量；
（2）行星表面的重力加速度是多少？

未来“嫦娥五号”落月后，轨道飞行器将作为中继卫星在绕月轨道上做圆周运动，如图所示．设卫星距离月球表面高为h，绕行周期为T，已知月球绕地球公转的周期为T₀，地球半径为R，地球表面的重力加速度为g，月球半径为r，万有引力常量为G．试分别求出：

（1）地球的质量和月球的质量；
（2）中继卫星向地球发送的信号到达地球，最少需要多长时间？（已知光速为c，且h≤r≤R）

2009年2月天文学家发现了COROT-7b，其密度和地球接近，直径大约是地球的两倍。假定它的密度和地球的平均密度相等，直径等于地球直径的两倍，人们可以在该行星表面进行如下的物理活动。如图，货物传送带与水平地面间的夹角为θ，且有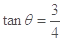，下端A与上端B之间的长度L=20m，传送带以v=8m/s的速度顺时针转动。将质量m=4kg的小物体轻放在传送带下端A处，物块与传送带之间的动摩擦因数μ=5/4。取地球表面重力加速度g= l0m/s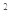，sinθ=0.6，cosθ=0.8，求：物块从A到B的过程中，传送带对物块做的功。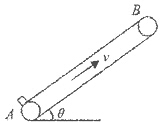

海王星有13颗已知的天然卫星。现认为海卫二绕海王星沿圆轨道匀速运转，已知海卫二的质量2.0×l0¹⁹kg，轨道半径为7.2×10⁶km，运行的周期为360天，万有引力常量G=6.67×l0^－1lN·m²/kg²,试估算海王星的质量。（结果保留一位有效数字）

在勇气号火星探测器着陆的最后阶段，着陆器降落到火星表面上，再经过多次弹跳才停下来。假设着陆器第一次落到火星表面弹起后，到达最高点时高度为h，速度方向是水平的，速度大小为v₀，求它第二次落到火星表面时速度的大小，计算时不计火星大气阻力。已知火星的一个卫星的圆轨道的半径为r，周期为T，火星可视为半径为r₀的均匀球体。

经过用天文望远镜长期观测，人们在宇宙中已经发现了许多双星系统，通过对它们的研究，使我们对宇宙中物质的存在形式和分布情况有了较深刻的认识，双星系统由两个星体组成，其中每个星体的线度都远小于两星体之间的距离，一般双星系统距离其他星体很远，可以当做孤立系统来处理。现根据对某一双星系统的光度学测量确定，该双星系统中每个星体的质量都是M，两者相距L，它们正围绕两者连线的中点做圆周运动。试求：
（1）该双星系统的运动周期；
（2）若该实验中观测到的运动周期为T_观测，且。为了理解T_观测 与T_计算的不同，目前有一种流行的理论认为，在宇宙中可能存在一种望远镜观测不到的暗物质。作为一种简化模型，我们假定在以这两个星体连线为直径的球体内均匀分布这种暗物质。若不考虑其他暗物质的影响，根据这一模型和上述观测结果确定该星系间这种暗物质的密度。

我国“神舟”五号飞船于2003年l0月15日在酒泉航天发射场由长征二号F运载火箭成功发射升空，若长征二号F运载火箭和飞船起飞时总质量为1.0×10⁵kg，起飞推动力为3.0×10⁶N，运载火箭发射塔高160m，试问：（g=10m/s²）
（1）运载火箭起飞时的加速度为多大？
（2）假如运载火箭起飞时推动力不变，忽略一切阻力和运载火箭质量的变化，试确定运载火箭需经多长时间才能飞离发射塔？
（3）这段时间内飞船中的宇航员承受了多大的压力？（设宇航员的质量为65kg）

在半径R＝5000 km 的某星球表面，宇航员做了如下实验．实验装置如图甲所示，竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成，将质量m＝0.2 kg 的小球从轨道AB上高H处的某点静止滑下，用力传感器测出小球经过C点时对轨道的压力F，改变H的大小，可测出相应的F大小，F随H的变化关系如图乙所示．求：

（1）圆轨道的半径．
（2）该星球的第一宇宙速度．

如图所示，A是地球的同步卫星．另一卫星B的圆形轨道位于赤道平面内，离地面高度为h.已知地球半径为R，地球自转角速度为ω0，地球表面的重力加速度为g，O为地球中心．

(1)求卫星B的运行周期．
(2)如卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近(O、B、A在同一直线上)，则至少经过多长时间，它们还能相距最近？

一个质量为1500 kg行星探测器从某行星表面竖直升空，发射时发动机推力恒定，发射升空后8 s末，发动机突然间发生故障而关闭；如图所示为探测器从发射到落回出发点全过程的速度图象；已知该行星表面没有大气，不考虑探测器总质量的变化；求：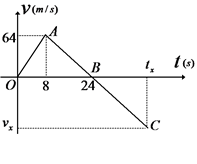

（1）探测器在行星表面上升达到的最大高度；
（2）探测器落回出发点时的速度；
（3）探测器发动机正常工作时的推力。

我国自主研制的北斗卫星导航系统包括5颗静止轨道卫星（同步卫星）和30颗非静止轨道卫星，将为全球用户提供高精度、高可靠性的定位、导航服务。
A为地球同步卫星，质量为m₁；B为绕地球做圆周运动的非静止轨道卫星，质量为m₂，离地面高度为h.已知地球半径为R，地球自转周期为T₀，地球表面的重力加速度为g。 求：
(1)卫星A运行的角速度；(2)卫星B运行的线速度。