质量为m的卫星发射前静止在地球赤道表面。假设地球可视为质量均匀分布的球体,半径为R。
(1)已知地球质量为M,自转周期为T,引力常量为G。求此时卫星对地表的压力N的大小;
(2)卫星发射后先在近地轨道上运行(轨道离地面的高度可以忽略不计),运行的速度大小为v1,之后经过变轨成为地球的同步卫星,此时离地面高度为H,运行的速度大小为v2。
a.求比值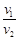 ;
;
b.若卫星发射前随地球一起自转的速度大小为v0,通过分析比较v0、 v1、v2三者的大小关系。
相关知识点
质量为m的卫星发射前静止在地球赤道表面。假设地球可视为质量均匀分布的球体,半径为R。
(1)已知地球质量为M,自转周期为T,引力常量为G。求此时卫星对地表的压力N的大小;
(2)卫星发射后先在近地轨道上运行(轨道离地面的高度可以忽略不计),运行的速度大小为v1,之后经过变轨成为地球的同步卫星,此时离地面高度为H,运行的速度大小为v2。
a.求比值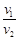 ;
;
b.若卫星发射前随地球一起自转的速度大小为v0,通过分析比较v0、 v1、v2三者的大小关系。