(本小题满分13分)某园林公司计划在一块 为圆心,
为圆心, (
( 为常数,单位为米)为半径的半圆形(如图)地上种植花草树木,其中弓形
为常数,单位为米)为半径的半圆形(如图)地上种植花草树木,其中弓形 区域用于观赏样板地,
区域用于观赏样板地, 区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
(1)设 , 用
, 用 表示弓形
表示弓形 的面积
的面积 ;
;
(2)园林公司应该怎样规划这块土地,才能使总利润最大? 并求相对应的
(本小题满分13分)已知曲线 ,从
,从 上的点
上的点 作
作 轴的垂线,交
轴的垂线,交 于点
于点 ,再从点
,再从点 作
作 轴的垂线,交
轴的垂线,交 于点
于点 ,设
,设
 .
.
(1)求数列 的通项公式;
的通项公式;
(2)记 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: ;
;
(3)若已知 ,记数列
,记数列 的前
的前 项和为
项和为 ,数列
,数列 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小.
的大小.
(本小题满分13分)对于给定数列 ,如果存在实常数
,如果存在实常数 ,使得
,使得 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列 是 “M类数列”.
是 “M类数列”.
(I)若 ,
, ,
, ,数列
,数列 、
、 是否为“M类数列”?若是,指出它对应的实常数
是否为“M类数列”?若是,指出它对应的实常数 ,若不是,请说明理由;
,若不是,请说明理由;
(II)若数列 满足
满足 ,
, .
.
(1)求数列 前
前 项的和.
项的和.
(2)已知数列 是 “M类数列”,求
是 “M类数列”,求 .
.
把正整数1,2,3,4,5,6,……按某种规律填入下表,
| |
第一列 |
第二列 |
第三列 |
第四列 |
第五列 |
第六列 |
第七列 |
第八列 |
第九列 |
第十列 |
 |
 |
| 第一行 |
|
2 |
|
|
6 |
|
|
10 |
|
|
 14 14 |
|
| 第二行 |
1 |
|
4 |
5 |
|
8 |
9 |
|
12 |
13 |
|
 |
| 第三行 |
|
3 |
|
|
7 |
|
|
11 |
|
|
15 |
|
按照这种规律继续填写,2011出现在第______行第______列( ).
A.第1行第1506列 B.第3行第1508列
C.第2行第1507列  D.第3行第1507列
D.第3行第1507列
在R上定义运算△: 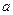 △
△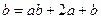 ,则满足
,则满足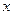 △
△ <0的实数
<0的实数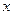 的取值范围为( )
的取值范围为( )
| A.(0,2) | B.(-2,1) | C.(-∞,-2)∪(1,+∞) | D.(-1,2) |
从装有2个红球和2个黑球的口袋内任取2个球,那么互斥而不对立的两个事件是( )
| A.恰有1个黑球与恰有2个黑球 | B.至少有1个黑球与至少有1个红球 |
| C.至少有1个黑球与都是黑球 | D.至少有1个黑球与都是红球 |