从区间 随机抽取2 n个数 , ,…, , , ,…, ,构成 n个数对 , ,…, ,其中两数的平方和小于1的数对共有 m个,则用随机模拟的方法得到的圆周率 的近似值为( )
| A. |
|
B. |
|
C. |
|
D. |
|
中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的 , ,依次输入的a为2,2,5,则输出的 ( )
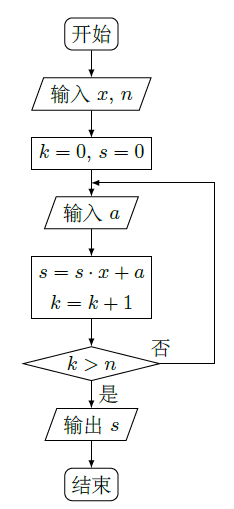
| A. | 7 |
B. | 12 |
C. | 17 |
D. | 34 |
若将函数 的图像向左平移 个单位长度,则评议后图象的对称轴为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )
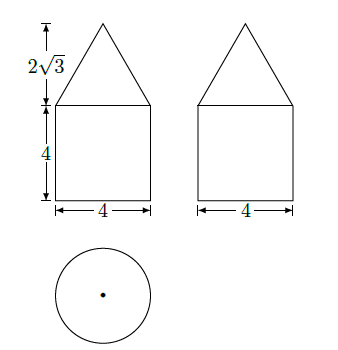
| A. |
|
B. |
|
C. |
|
D. |
|
如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )
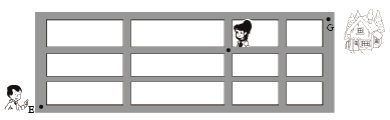
| A. |
24 |
B. |
18 |
C. |
12 |
D. |
9 |
已知 在复平面内对应的点在第四象限,则实数m的取值范围是( )
| A. |
|
B. |
|
C. |
|
D. |
|
设函数 ,其中 。
(1)求 的单调区间;
(2)若 存在极点 , 且 ,其中 , 求证: ;
(3)设 ,函数 ,求证: 在区间 上的最大值不小于 .
设椭圆 的右焦点为F,右顶点为A,已知 ,其中O为原点,e为椭圆的离心率.
(1)求椭圆的方程;
(2)设过点A的直线l与椭圆交于B(B不在 轴上),垂直于l的直线与l交于点M,与y轴交于点H,若 ,且 ,求直线 的斜率.
已知 是各项均为整数得等差数列,公差为d,对任意的 , 是 和 得等比中项。
(1)设 , ,求证:数列 是等差数列;
(2)设 , , ,求证:
如图,正方形 的中心为 ,四边形 为矩形,平面 平面 , 点 为 的中点,
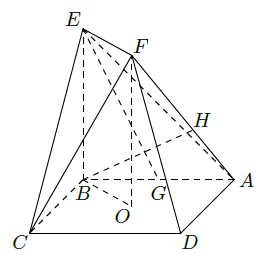
(1)求证: 平面 ;
(2)求二面角 的正弦值;
(3)设 H为线段 上的点,且 ,求直线 和平面 所成角的正弦值.