已知O为坐标原点,F是椭圆 的左焦点,A,B分别为C的左,右顶点.P为C上一点,且 轴,过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为( )
| A. |
|
B. |
|
C. |
|
D. |
|
在封闭的直三棱柱 内有一个体积为V的球,若 , , , ,则 的最大值是( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )

| A. |
|
B. |
|
C. |
90 |
D. |
81 |
执行如图程序框图,如果输入的 , ,那么输出的 ( )
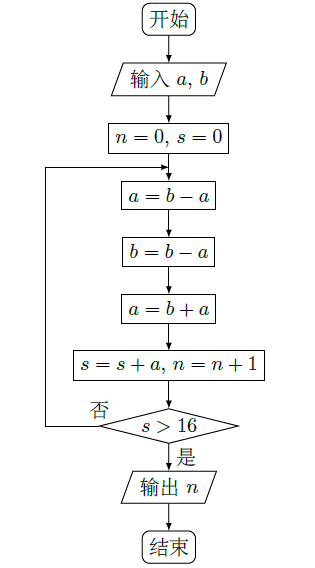
| A. | 3 |
B. | 4 |
C. | 5 |
D. | 6 |
小敏打开计算机时,忘记了开机密码的前两位,只记得第一位是M,I,N中的一个字母,第二位是1,2,3,4,5中的一个数字,则小敏输入一次密码能够成功开机的概率是( )
| A. |
|
B. |
|
C. |
|
D. |
|
某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图,图中A点表示十月的平均最高气温约为 ,B点表示四月的平均最低气温约为 ,下面叙述不正确的是( )
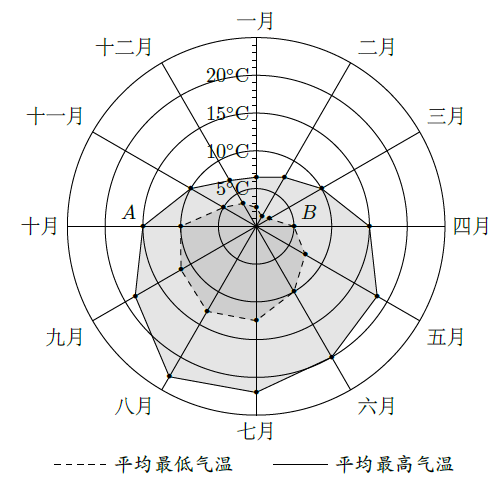
| A. | 各月的平均最低气温都在 以上 |
B. | 七月的平均温差比一月的平均温差大 |
| C. | 三月和十一月的平均最高气温基本相同 |
D. | 平均最高气温高于 的月份有5个 |
设定义在R上的函数 满足:对于任意的x 1、x 2∈R,当 时,都有 .
(1)若 ,求a的取值范围;
(2)若 是周期函数,证明: 是常值函数;
(3)设 恒大于零, 是定义在R上的、恒大于零的周期函数,M是 的最大值.函数 .证明:" 是周期函数"的充要条件是" 是常值函数".
在平面直角坐标系xOy中,已知椭圆Γ: ,A为Γ的上顶点,P为Γ上异于上、下顶点的动点,M为x正半轴上的动点.
(1)若P在第一象限,且|OP|= ,求P的坐标;
(2)设P ,若以A、P、M为顶点的三角形是直角三角形,求M的横坐标;
(3)若 ,直线AQ与Γ交于另一点C,且 , ,求直线AQ的方程.