(本小题12分)某电视节目《幸运猜猜猜》有这样一个竞猜环节,一件价格为9816元的商品,选手只知道1,6,8,9四个数,却不知其顺序,若在竞猜中猜出正确价格中的两个或以上(但不含全对)正确位置,则正确位置会点亮红灯作为提示;若全对,则所有位置全亮白灯并选手赢得该商品,
(Ⅰ)求某选手在第一次竞猜时,亮红灯的概率;
(Ⅱ)若该选手只有二次机会,则他赢得这件商品的概率为多少?
(本小题12分)设△ABC的内角A,B,C所对的边长分别为a,b,c,且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若角 ,
, 边上的中线
边上的中线 的长为
的长为 ,求
,求 的面积.
的面积.
抛物线 过焦点F的直线
过焦点F的直线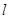 交抛物线于A、B两点,O为原点,若
交抛物线于A、B两点,O为原点,若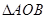 面积最小值为8。
面积最小值为8。
(1)求P值
(2)过A点作抛物线的切线交y轴于N, 则点M在一定直线上,试证明之。
则点M在一定直线上,试证明之。
设等差数列 的前
的前 项和为
项和为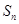 ,公比是正数的等比数列
,公比是正数的等比数列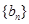 的前
的前 项和为
项和为 ,已知
,已知
(1)求 的通项公式。
的通项公式。
(2)若数列 满足
满足 求数列
求数列 的前
的前 项和
项和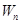 。
。
已知函数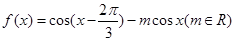 的图象过
的图象过 ,且
,且 内角A、B、C所对应边分别为a、b、c,若
内角A、B、C所对应边分别为a、b、c,若
①求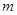 的值及
的值及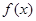 的单调递增区间
的单调递增区间
②求 的面积。
的面积。
如图,在四棱锥 中,
中, 平面
平面 四边形
四边形 为正方形,
为正方形, 点在
点在 上的射影为
上的射影为 点.
点.
(1)求证: 平面
平面
(2)在棱 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 .若存在,求出
.若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
在如图所示的空间几何体中,平面 平面
平面

 =
= ,
, 和平面
和平面 所成的角为
所成的角为 ,且点
,且点 在平面
在平面 上的射影落在
上的射影落在 的平分线上.
的平分线上.
(I)求证: 平面
平面
(II)求二面角 的余弦值
的余弦值
对定义在区间l,上的函数 ,若存在开区间
,若存在开区间 和常数C,使得对任意的
和常数C,使得对任意的 都有
都有 ,且对任意的x
,且对任意的x (a,b)都有
(a,b)都有 恒成立,则称函数
恒成立,则称函数 为区间I上的“Z型”函数.
为区间I上的“Z型”函数.
(I)求证:函数 是R上的“Z型”函数;
是R上的“Z型”函数;
(Ⅱ)设 是(I)中的“Z型”函数,若不等式
是(I)中的“Z型”函数,若不等式 对任意的x
对任意的x R恒成立,求实数t的取值范围.
R恒成立,求实数t的取值范围.
在平面直角坐标系xOy中,已知圆锥曲线C的参数方程为 为参数).
为参数).
(I)以原点为极点,x轴正半轴为极轴建立极坐标系,求圆锥曲线C的极坐标方程;
(Ⅱ)若直线l过曲线C的焦点且倾斜角为60°,求直线l被圆锥曲线C所截得的线段的长度.
椭圆M的中心在坐标原点D,左、右焦点F1,F2在x轴上,抛物线N的顶点也在原点D,焦点为F2,椭圆M与抛物线N的一个交点为A(3, ).
).
(I)求椭圆M与抛物线N的方程;
(Ⅱ)在抛物线N位于椭圆内(不含边界)的一段曲线上,是否存在点B,使得△AF1B的外接圆圆心在x轴上?若存在,求出B点坐标;若不存在,请说明理由.