设函数
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)设 对任意
对任意 ,总有
,总有 成立,求实数a的取值范围;
成立,求实数a的取值范围;
(3)当 时,方程
时,方程 在区间
在区间 内有唯一实数解,求实数
内有唯一实数解,求实数 的取值范围.
的取值范围.
已知椭圆 的离心率为
的离心率为 ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.
(1)求椭圆C的方程;
(2)已知直线 与椭圆C交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与椭圆C交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
(本小题满分12分)设向量a=(4cosα,sinα),b=(sinβ,4cosβ),c=(cosβ,-4sinβ),
(1)若a与b-2c垂直,求tan(α+β)的值;
(2)求|b+c|的最大值.
某种产品的广告费支出 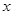 与销售额
与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
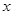 |
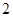 |
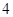 |
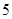 |
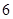 |
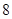 |
 |
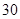 |
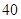 |
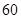 |
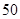 |
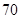 |
参考数据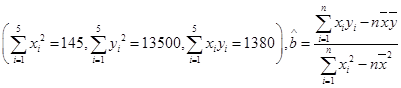
(1)求线性回归方程;
(2)试预测广告费支出为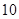 百万元时,销售额多大?
百万元时,销售额多大?
已知直线 :
: (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为 .
.
(1)将曲线C的极坐标方程化为直坐标方程;
(2)设点M的直角坐标为 ,直线l与曲线C的交点为A,B,求|MA|•|MB|的值.
,直线l与曲线C的交点为A,B,求|MA|•|MB|的值.
如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD.
某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校 学年高二年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在
学年高二年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在 分下的学生后,共有男生
分下的学生后,共有男生 名,女生
名,女生 名,现采用分层抽样的方法,从中抽取了
名,现采用分层抽样的方法,从中抽取了 名学生,按性别分为两组,并将两组学生成绩分为
名学生,按性别分为两组,并将两组学生成绩分为 组,得到如下所示频数分布表.
组,得到如下所示频数分布表.
| 分数段 |
 |
 |
 |
 |
 |
 |
| 男 |
 |
 |
 |
 |
 |
 |
| 女 |
 |
 |
 |
 |
 |
 |
(1)估计男、女生各自的平均分(同一组数据用该级区间中点值作代表),从计算结果看,数学成绩与性别是否有关;
(2)规定 分以上者为优分(含
分以上者为优分(含 分),请你根据已知条件作出
分),请你根据已知条件作出 列联表,并判断是否有
列联表,并判断是否有 以上的把握认为“数学成绩与性别有关”.
以上的把握认为“数学成绩与性别有关”.
| |
优分 |
非优分 |
合计 |
| 男生 |
|
|
|
| 女生 |
|
|
|
| 合计 |
|
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

某种产品的广告费支出  与销售额
与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
 |
 |
 |
 |
 |
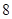 |
 |
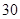 |
 |
 |
 |
 |
参考数据
(1)求线性回归方程;
(2)试预测广告费支出为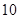 百万元时,销售额多大?
百万元时,销售额多大?
某商场的销售部经过市场调查发现,该商场的某种商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 ,其中
,其中 ,
, 为常数,已知销售价格为
为常数,已知销售价格为 元/千克时,每日可售出该商品
元/千克时,每日可售出该商品 千克.
千克.
(Ⅰ)求 的值;
的值;
(Ⅱ)若该商品的成本为 元/千克,试确定销售价格
元/千克,试确定销售价格 的值,使该商场每日销售该商品所获得的利润最大.
的值,使该商场每日销售该商品所获得的利润最大.
为了促进学生的全面发展,某市教育局要求本市所有学校重视社团文化建设,2014年该市某中学的某新生想通过考核选拨进入该校的“电影社”和“心理社”,已知该同学通过考核选拨进入这两个社团成功与否相互独立.根据报名情况和他本人的才艺能力,两个社团都能进入的概率为 ,至少进入一个社团的概率为
,至少进入一个社团的概率为 ,并且进入“电影社”的概率小于进入“心理社”的概率.
,并且进入“电影社”的概率小于进入“心理社”的概率.
(Ⅰ)求该同学分别通过选拨进入“电影社”的概率 和进入“心理社”的概率
和进入“心理社”的概率 ;
;
(Ⅱ)学校根据这两个社团的活动安排情况,对进入“电影社”的同学增加1个校本选修课学分,对进入“心理社”的同学增加0.5个校本选修课学分.求该同学在社团方面获得校本选修课学分分数的分布列和数学期望.