为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.
(1)根据二维条形图,完形填空2×2列联表:
(2)对照如表,利用列联表的独立性检验估计,请问有多大把握认为“性别与喜欢数学有关系”?
已知等差数列{an}满足a3=5,a5﹣2a2=3,又等比数列{bn}中,b1=3且公比q=3.
(1)求数列{an},{bn}的通项公式;
(2)若cn=an+bn,求数列{cn}的前n项和Sn.
已知全集U=R,A={x|﹣3<x≤6,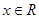 },B={x|x2﹣5x﹣6<0,
},B={x|x2﹣5x﹣6<0,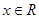 }.求:
}.求:
(1)A∪B;
(2)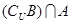 .
.
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位,已知直线  的参数方程为
的参数方程为  (t为参数,
(t为参数,  ),曲线C的极坐标方程为
),曲线C的极坐标方程为 .
.
(Ⅰ)求曲线C的直角坐标方程。
(Ⅱ)设直线  与曲线C相交于A,B两点,当a变化时,求
与曲线C相交于A,B两点,当a变化时,求  的最小值
的最小值
为了检验“喜欢玩手机游戏与认为作业多”是否有关系,某班主任对班级的30名学生进行了调查,得到一个2×2列联表:
| |
认为作业多 |
认为作业不多 |
合计 |
| 喜欢玩手机游戏 |
18 |
2 |
|
| 不喜欢玩手机游戏 |
|
6 |
|
| 合计 |
|
|
30 |
(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程);
(Ⅱ)能否在犯错误的概率不超过0.005的前提下认为“喜欢玩手机游戏”与“认为作业多”有关系?
(Ⅲ)若从不喜欢玩手机游戏的人中随机抽取3人,则至少2人认为作业不多的概率是多少?
已知三角形的三个顶点是A(4,0),B(6,6),C(0,2).
(1)求AB边上的高所在直线的方程;
(2)求AC边上的中线所在直线的方程.
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数字为茎,个位数字为叶得到的茎叶图如图所示.已知甲、乙两组数据的平均数都为10.
(1)求 的值;
的值;
(2)分别求出甲、乙两组数据的方差 和
和 ,
,
并由此分析两组技工的加工水平;
(3)质检部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人加工的合格零件数之和大于17,则称该车间“质量合格”,求该车间“质量合格”的概率.
(注:方差 ,
, 为数据
为数据 的平均数)
的平均数)
已知函数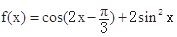 ,
,
(1)求函数f(x)的最大值和最小正周期;(2)若a为锐角,且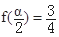 ,求sina的值.
,求sina的值.