广东省清远市高二下学期期末文科数学试卷
已知集合A={0,1,2},B={x|1<x<4},则A∩B=( )
| A.{0} | B.{1} | C.{2} | D.{1,2} |
如图是集合的知识结构图,如果要加入“全集”,则应该放在( )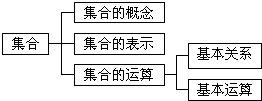
| A.“集合的概念”的下位 | B.“集合的表示”的下位 |
| C.“基本关系”的下位 | D.“基本运算”的下位 |
已知p:x=2,q:0<x<3,则p是q的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分,又不必要条件 |
用反证法证明命题“若 a,b∈N,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为( )
| A.a,b都能被3整除 | B.a不能被3整除 |
| C.a,b不都能被3整除 | D.a,b都不能被3整除 |
演绎推理“因为对数函数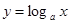 (a>0且a≠1)是增函数,而函数
(a>0且a≠1)是增函数,而函数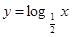 是对数函数,所以
是对数函数,所以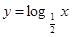 是增函数”所得结论错误的原因是( )
是增函数”所得结论错误的原因是( )
| A.大前提错误 | B.小前提错误 |
| C.推理形式错误 | D.大前提和小前提都错误 |
设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则 ,类比这个结论可知:四面体S﹣ABC的四个面的面积分别为S1、S2、S3、S4,内切球半径为r,四面体S﹣ABC的体积为V,则r=( )
,类比这个结论可知:四面体S﹣ABC的四个面的面积分别为S1、S2、S3、S4,内切球半径为r,四面体S﹣ABC的体积为V,则r=( )
A. |
B. |
C. |
D. |
函数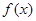 在定义域R内可导,若
在定义域R内可导,若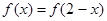 ,且
,且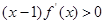 ,若
,若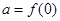 ,
,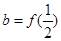 ,
,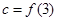 ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )
| A.a>b>c | B.c>a>b | C. B>a>c | D.c>b>a |
如图,在△ABC中,AB=8,AC=7,BC=6,D是AB的中点,∠ADE=∠ACB,则DE= _________ .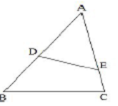
如图,⊙O上一点C在直径AB上的射影为D,AC=4,AD=2,则⊙O的面积是 _________ .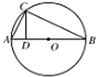
如图,AC为⊙O的直径,OB⊥AC,弦BN交AC于点M.若OC= ,OM=1,则MN= _________ .
,OM=1,则MN= _________ .
在极坐标系中,圆C的方程为ρ=1,直线l的方程为ρsin(θ+ )=
)= ,则圆心C到直线l的距离为 _________ .
,则圆心C到直线l的距离为 _________ .
为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.
(1)根据二维条形图,完形填空2×2列联表:
(2)对照如表,利用列联表的独立性检验估计,请问有多大把握认为“性别与喜欢数学有关系”?
某同学在研究性学习中,收集到某制药厂车间工人数(单位:十人)与药品产量(单位:万盒)的数据如表所示:
| 工人数:x(单位:十人) |
1 |
2 |
3 |
4 |
| 药品产量:y(单位:万盒) |
3 |
4 |
5 |
6 |
(1)请画出如表数据的散点图;
(2)参考公式,根据表格提供的数据,用最小二乘法求出y关于x的线性回归方程y= x+
x+ ;(参考数据
;(参考数据 i2=30,
i2=30, xiyi=50)
xiyi=50)
(3)试根据(2)求出的线性回归方程,预测该制药厂车间工人数为45时,药品产量是多少?
在△ABC中,角A、B、C的对边分别为a、b、c,且角A、B都是锐角,a=6,b=5, .
.
(1)求 和
和 的值;
的值;
(2)设函数 ,求
,求 的值.
的值.
如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B﹣ACD,点M是棱BC的中点,DM=2 .
.
(1)求证:OM∥平面ABD;
(2)求证:平面DOM⊥平面ABC;
(3)求三棱锥B﹣DOM的体积.
已知抛物线 与双曲线
与双曲线 有公共焦点
有公共焦点 .点
.点 是曲线C1,C2在第一象限的交点,且
是曲线C1,C2在第一象限的交点,且 .
.
(1)求双曲线交点 及另一交点
及另一交点 的坐标和点
的坐标和点 的坐标;
的坐标;
(2)求双曲线 的方程;
的方程;
(3)以 为圆心的圆M与直线
为圆心的圆M与直线 相切,圆N:
相切,圆N: ,过点P(1,
,过点P(1, )作互相垂直且分别与圆M、圆N相交的直线
)作互相垂直且分别与圆M、圆N相交的直线 和
和 ,设
,设 被圆M截得的弦长为s,
被圆M截得的弦长为s, 被圆N截得的弦长为t,问:
被圆N截得的弦长为t,问: 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
 的值为( )
的值为( )


 ,则
,则 ,
, ,
, ,
, ,由此可以归纳出( )
,由此可以归纳出( )



 (
( 是虚数单位),则
是虚数单位),则 _________ .
_________ . ,
, ),那么它的直角坐标系表示为 _________ .
),那么它的直角坐标系表示为 _________ .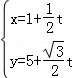 (t为参数)化成普通方程为 _________ .
(t为参数)化成普通方程为 _________ . 的前
的前 项和为
项和为 ,
, ,函数
,函数 .
. 的值和数列
的值和数列 时,
时, ;
; .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号