设f(x)=a(x﹣5)2+6lnx,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值.
若直线 与曲线C满足下列两个条件:(i)直线
与曲线C满足下列两个条件:(i)直线 在点
在点 处与曲线C相切;(ii)曲线C在点
处与曲线C相切;(ii)曲线C在点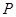 附近位于直线
附近位于直线 的两侧,则称直线
的两侧,则称直线 在点
在点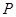 处“切过”曲线C,下列命题正确的是________(写出所有正确命题的编号).
处“切过”曲线C,下列命题正确的是________(写出所有正确命题的编号).
①直线 在点
在点 入“切过”曲线
入“切过”曲线
②直线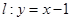 在点
在点 处“切过”曲线
处“切过”曲线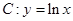
③直线 在点
在点 处“切过”曲线
处“切过”曲线
④直线 在点
在点 处“切过”曲线
处“切过”曲线
已知函数 ,
,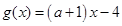 .
.
(1)当 时,求函数
时,求函数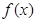 在
在 处的切线方程;
处的切线方程;
(2)是否存在实数 ,使得对任意的
,使得对任意的 ,恒有
,恒有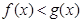 成立?若存在,求出实数
成立?若存在,求出实数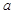 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.