高中数学组合几何解答题

(本题满分14分)
已知函数其中实数。
(1)-2，求曲线在点处的切线方程；
(2)x=1处取得极值，试讨论的单调性。

已知函数（），且.
（Ⅰ）试用含有的式子表示，并求的极值；
（Ⅱ）对于函数图象上的不同两点，，如果在函数图象上存在点（其中），使得点处的切线，则称存在“伴随切线”. 特别地，当时，又称存在“中值伴随切线”. 试问：在函数的图象上是否存在两点、使得它存在“中值伴随切线”，若存在，求出、的坐标，若不存在，说明理由.

（本小题共14分）已知函数（）.
（1）若函数的图象在点处的切线的倾斜角为，求；
（2）若存在，使，求的取值范围.

（本小题满分12分）
已知函数，若图象上的点处的切线斜率为，求在区间上的最值.

（本小题满分12分）
已知函数
（I）当时，求曲线在点处的切线方程；
（II）当时，讨论的单调性.

（本小题满分14分）已知：在函数的图象上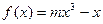，以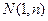为切点的切线的倾斜角为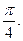
（I）求的值；
（II）是否存在最小的正整数，使得不等式恒成立？如果存在，请求出最小的正整数，如果不存在，请说明理由。

已知抛物线与直线相切于点．
（Ⅰ）求函数的解析式；
（Ⅱ）已知函数，求的值域.

已知函数
（1）求曲线在点处的切线的方程；
（2）直线为曲线的切线，且经过原点，求直线的方程及切点坐标。

已知是实数，函数
（1）若，求的值及曲线在点（1、）处的切线方程。
（2）求在区间[0、2]上的最大值。

（本小题满分12分）
已知函数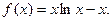
（I）求函数处的切线的方程；
（II）设实数

设，函数．
（Ⅰ）若，求曲线在点处的切线方程；
（Ⅱ）求函数在上的最小值．

（满分12分）
已知曲线在第三象限
（1）求P₀的坐标；
（2）若直线的方程。

（本小题满分10分）
设函数若曲线的斜率最小的切线与直线平行，求
⑴的值
⑵函数的单调区间
⑶若在上恒成立，求c的取值范围

(本小题满分12分)
已知函数.
（1）若点()为函数与的图象的公共点，试求实数的值；
（2）设是函数的图象的一条对称轴，求的值;
（3）求函数的值域。

16. （本小题满分14分)
两条曲线  都经过点, 并且它们在点处有公共的切线，求，，的值。