新课标版广东省遂溪县高一数学必修一(函数、导数、方程与不等式)单元测试
若函数 在(1,2)内有极小值,则实数a的取值范围是( )
在(1,2)内有极小值,则实数a的取值范围是( )
A. |
B. |
C. |
D. |
已知 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 的最大值是4,则
的最大值是4,则 的最大值是( )
的最大值是( )
| A.4 | B. |
C.1 | D. |
函数 有且仅有一个正实数的零点,则实数
有且仅有一个正实数的零点,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
定义在R上的偶函数 的部分图像如右图所示,则在区间
的部分图像如右图所示,则在区间 上,下列函数中与
上,下列函数中与 的单调性不同的是( )
的单调性不同的是( )
A. |
B. |
C. |
D. |
 |
设函数 的定义域分别为F、G,且F G。若对任意的
的定义域分别为F、G,且F G。若对任意的 ,都有
,都有 ,则称
,则称 在G上的一个“延拓函数”。已知函数
在G上的一个“延拓函数”。已知函数 在R上一个延拓函数,且g(x)是偶函数,则函数g(x)的解析式是 ( )
在R上一个延拓函数,且g(x)是偶函数,则函数g(x)的解析式是 ( )
A. |
B. |
C. |
D. |
已知函数 的定义域为
的定义域为 ,导函数为
,导函数为 且
且 ,则满足
,则满足 的实数
的实数 的取值范围为( )
的取值范围为( )
A. |
B. ) ) |
C. |
D. ) ) |
右图是函数 的导函数
的导函数 的图象.
的图象.
给出下列命题:
① 是函数
是函数 的极值点;
的极值点;
② 是函数
是函数 的极值点;
的极值点;
③ 在
在 处切线的斜率小于零;
处切线的斜率小于零;
④ 在区间
在区间 上单调递增.
上单调递增.
则正确命题的序号是 .(请写出所有正确命题的序号) 
已知函数 是定义在
是定义在 上的偶函数,若对于任意
上的偶函数,若对于任意 ,都有
,都有 ,且当
,且当 时,
时, ,则
,则 的值为__________.
的值为__________.
设二次函数 在区间
在区间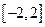 上的最大值、最小值分别是M、m,集合
上的最大值、最小值分别是M、m,集合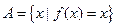 .若
.若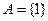 ,且
,且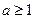 ,记
,记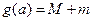 ,则
,则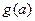 的最小值 。
的最小值 。
已知函数 的图象过点
的图象过点 ,且它在
,且它在 处的切线方程为
处的切线方程为 .
.
若对任意 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的取值范围__________..
的取值范围__________..
已知函数 .
.
(1)当a = 4,解不等式 ;
;
(2)若函数 是奇函数,求a的值;
是奇函数,求a的值;
(3)若不等式 在
在 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
若关于 的实系数方程
的实系数方程 有两个根,一个根在区间
有两个根,一个根在区间 内,另一根在区间
内,另一根在区间 内,记点
内,记点 对应的区域为
对应的区域为 .
.
(1)设 ,求
,求 的取值范围;
的取值范围;
(2)过点 的一束光线,射到
的一束光线,射到 轴被反射后经过区域
轴被反射后经过区域 ,求反射光线所在直线
,求反射光线所在直线 经过区域
经过区域 内的整点(即横纵坐标为整数的点)时直线
内的整点(即横纵坐标为整数的点)时直线 的方程.
的方程.
已知函数 .
.
(I)若函数 在点
在点 处的切线斜率为4,求实数
处的切线斜率为4,求实数 的值;
的值;
(II)若函数 在区间
在区间 上存在零点,求实数
上存在零点,求实数 的取值范围
的取值范围
设 ,函数
,函数 .
.
(Ⅰ)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求函数 在
在 上的最小值.
上的最小值.
已知定义在 上的奇函数
上的奇函数 在
在 处取得极值.
处取得极值.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)试证:对于区间 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 成立;
成立;
(Ⅲ)若过点 可作曲线
可作曲线 的三条切线,试求点P对应平面区域的面积.
的三条切线,试求点P对应平面区域的面积.

 若
若 则实数a的取值范围是( )
则实数a的取值范围是( )



 则
则  ( )
( )



 在
在 时为减函数,则m= 。
时为减函数,则m= 。 ,若
,若
 = 。
= 。 ,
,
 的单调区间。
的单调区间。 )处的切线的倾斜角为
)处的切线的倾斜角为 ,对任意的
,对任意的 ,函数
,函数 在区间
在区间 上总不是单调函数,求m取值范围
上总不是单调函数,求m取值范围
 粤公网安备 44130202000953号
粤公网安备 44130202000953号