设函数f(x)=ax2+bx+c(a,b,c∈R),若x=-1为函数f(x)ex的一个极值点,则下列图象不可能为y=f(x)的图象是( ).
已知函数 在R上满足f(x)=2f(4-x)-2x2+5x,则曲线
在R上满足f(x)=2f(4-x)-2x2+5x,则曲线 在点(2,f(2) )
在点(2,f(2) )
处的切线方程是( )
| A.y=-x | B. |
C.y="-x" +4 | D.y="-2x+2" |
设曲线 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线 垂直,则
垂直,则
| A.2 | B. |
C. |
D. |
若过点 的直线与曲线
的直线与曲线 和
和 都相切,则
都相切,则 的值为 ( )
的值为 ( )
| A.2 | B. |
C.2或 |
D.3或 |
若过点 的直线与曲线
的直线与曲线 和
和 都相切,则
都相切,则 的值为( )
的值为( )
A.2或 |
B.3或 |
C.2 | D. |
函数 是定义在R上的可导函数,则下列说法不正确的是( )
是定义在R上的可导函数,则下列说法不正确的是( )
A.若函数在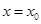 时取得极值,则 时取得极值,则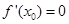 |
B.若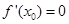 ,则函数在 ,则函数在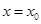 处取得极值 处取得极值 |
C.若在定义域内恒有 ,则 ,则 是常数函数 是常数函数 |
D.函数 在 在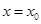 处的导数是一个常数 处的导数是一个常数 |