高中数学组合几何试题

设函数，曲线在点处的切线方程为，则曲线在点处切线的斜率为(     )                                          

A．

B．2

C．4

D．

曲线在点处的切线方程为________． 

，，
1）若求的极值
2）若在处的切线方程为，求实数的值

（1）已知函数f(x)=x－ax+(a－1)，。讨论函数的单调性；       
（2）.已知函数f (x)=lnx，g(x)=e^x．设直线l为函数 y＝f (x) 的图象上一点A(x₀，f (x₀))处的切线．问在区间(1，+∞)上是否存在x₀，使得直线l与曲线y=g(x)也相切．若存在，这样的x₀有几个？，若没有，则说明理由。

设函数（Ⅰ）当时，求曲线在点处的切线方程；
（Ⅱ）有三个不同的实数解，求的取值范围.

设函数 $f\left(x\right)=a\ln x+\frac{1}{2x}+\frac{3}{2}x+1$，其中在 $a\in R$，曲线 $y=f\left(x\right)$在点 $(1,f(1\left)\right)$处的切线垂直于 $x$轴
（Ⅰ）求 $a$的值；
（Ⅱ）求函数 $f\left(x\right)$极值．

若，则的值为（  ）

A．-2

B．2

C．-1

D．1

已知函数.
（1）若曲线在处的切线的方程为，求实数a的值；
（2）求证：≥0恒成立的充要条件是；
（3）若，且对任意，都有，求实数a的取值范围.

已知函数的导数满足，，其中常数，求曲线在点处的切线方程.

已知函数 ()
（1）若函数的图象在处的切线方程为，求的值；
（2）若函数在为增函数，求的取值范围．

设函数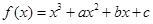的图象如图所示，且与在原点相切，若函数的极小值为，（1）求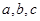的值；（2）求函数的递减区间．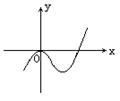

已知曲线f (x ) = ax ² ＋2在x=1处的切线与2x-y+1=0平行.
求由曲线y="f" (x ) 与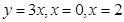所围成的平面图形的面积.

已知函数，．
（Ⅰ）若函数在处取得极值，试求的值，并求在点处的切线方程；
（Ⅱ）设，若函数在上存在单调递增区间，求的取值范围．

已知函数的导数满足，，其中常数，求曲线在点处的切线方程.

已知函数在处取得极值，过点作曲线的切线,（1）求此切线的方程.（2）求切线与函数的图象围成的平面图形的面积。