(本小题满分12分)
设函数 .
.
⑴ 当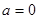 时,求函数
时,求函数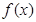 在点
在点 处的切线方程;
处的切线方程;
⑵ 对任意的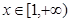 函数
函数 恒成立,求实数
恒成立,求实数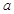 的取值范围.
的取值范围.
已知函数 .(I)当
.(I)当 时,求函数
时,求函数 的单调区间;(II)若函数
的单调区间;(II)若函数 的图象在点
的图象在点 处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的
处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的 ,函数
,函数 在区间
在区间 上总存在极值?
上总存在极值?
已知函数
 ).
).
(Ⅰ) 若 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(Ⅱ) 若函数 在其图象上任意一点
在其图象上任意一点 处切线的斜率都小于
处切线的斜率都小于 ,求实数
,求实数 的取值范围.
的取值范围.
已知 ,函数
,函数 ,
, (其中
(其中 为自然对数的底数).
为自然对数的底数).
(Ⅰ)判断函数 在
在 上的单调性;
上的单调性;
(II)是否存在实数 ,使曲线
,使曲线 在点
在点 处的切线与
处的切线与 轴垂直? 若存在,
轴垂直? 若存在,
求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)若实数 满足
满足 ,求证:
,求证: .
.
(本小题满分12分)
已知函数 且导数
且导数 .
.
(1)试用含有 的式子表示
的式子表示 ,并求
,并求 的单调区间;
的单调区间;
(2)对于函数图象上不同的两点 ,且
,且 ,如果在函数图像上存在点
,如果在函数图像上存在点 (其中
(其中 )使得点
)使得点 处的切线
处的切线 ,则称
,则称 存在“相依切线”.特别地,当
存在“相依切线”.特别地,当 时,又称
时,又称 存在“中值相依切线”.试问:在函数
存在“中值相依切线”.试问:在函数 上是否存在两点
上是否存在两点 使得它存在“中值相依切线”?若存在,求
使得它存在“中值相依切线”?若存在,求 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(本小题满分14分)已知函数 ,
, 是常数.
是常数.
(Ⅰ) 证明曲线 在点
在点 的切线经过
的切线经过 轴上一个定点;
轴上一个定点;
(Ⅱ) 若 对
对 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(参考公式: )
)
(Ⅲ)讨论函数 的单调区间.
的单调区间.
(本小题满分14分)
已知函数 .
.
(Ⅰ)若曲线 在点
在点 处的切线与直线
处的切线与直线 垂直,求实数
垂直,求实数 的值;
的值;
(Ⅱ)讨论函数 的单调性;
的单调性;
(Ⅲ)当 时,记函数
时,记函数 的最小值为
的最小值为 ,求证:
,求证: .
.
(满分14分)已知定义在正实数集上的函数 ,
, ,其中
,其中 .
.
设两曲线 ,
, 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(1)用 表示
表示 ;
;
(2)试证明不等式: (
( ).
).
设函数 ,曲线
,曲线 处的切线方程为
处的切线方程为 ,则曲线
,则曲线 处的切线方程为 ( )
处的切线方程为 ( )
A. |
B. |
C. |
D. |
曲线y="sinx+e" x在点(0,1)处的切线方程是( )
| A.x-3y+3=0 | B.x-2y+2=0 |
| C.2x-y+1="0" | D.3x-y+1=0 |
曲线3x2-y+6=0在x=- 处的切线的倾斜角是
处的切线的倾斜角是
A. π π |
B.- |
C. |
D.- π π |