[河南]2011-2012学年河南省周口市高二下学期四校第一次联考文科数学试卷
有一段演绎推理是这样的“有些有理数是真分数,整数是有理数,则整数是真分数”结论显然是错误的,是因为( )
| A.大前提错误 | B.小前提错误 |
| C.推理形式错误 | D.非以上错误 |
已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是( )
A. =1.23x+4 =1.23x+4 |
B. ="1.23x+5" ="1.23x+5" |
C. =1.23x+0.08 =1.23x+0.08 |
D. =0.08x+1.23 =0.08x+1.23 |
圆内接四边形ABCD中,∠A, ∠B, ∠C的度数的比是3:4:6,则∠D=( )
| A.60° | B.80° | C.120° | D.100° |
如图,在△ABC中,AB=3,AC=4,BC=5,AD平分∠BAC,则BD的值为( )
A. |
B. |
C. |
D. |

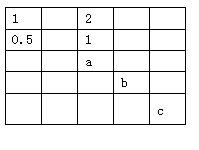
在下列表格中,每格填上一个数字后,使每一行成等差数列,每一列成等比数列,则a+b+c的值是( )
| A.1 | B.2 | C.3 | D.4 |
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是( )
| A.假设三内角都不大于60度 |
| B.假设三内角都大于60度 |
| C.假设三内角至多有一个大于60度 |
| D.假设三内角至多有两个大于60度 |
在复平面上的平行四边形ABCD中, 对应的复数是6+8i,
对应的复数是6+8i,  对应的复数是-4+6i.则
对应的复数是-4+6i.则 对应的复数是( )
对应的复数是( )
| A.2+14i | B.1+7i | C.2-14i | D.-1-7i |
观察 ,
, ,
, ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在 上的函数
上的函数 满足
满足 ,记
,记 为
为 的导函数,则
的导函数,则 =( )
=( )
A. |
B. |
C. |
D. |
已知,如图,在梯形ABCD中,AD//BC,AD=3,BC=7,点M,N分别是
对角线BD,AC的中点,则MN= ( )
| A.2 | B. 5 | C. |
D.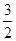 |

已知数列{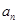 }的前
}的前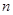 项和
项和 =
= (
(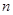 ≥2),而
≥2),而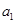 =1,通过计算
=1,通过计算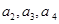 ,猜想
,猜想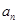 等于( )
等于( )
A. |
B.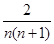 |
C.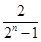 |
D.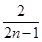 |
在边长分别为a, b, c的三角形ABC中,其内切圆半径为r,则该三角形面积S= (a+b+c)r,将这一结论类比到空间,有“若四面体A—BCD的四个面的面积分别为S
(a+b+c)r,将这一结论类比到空间,有“若四面体A—BCD的四个面的面积分别为S ,S
,S ,S
,S ,S
,S ,内切球半径为r,则四体的体积”为: .
,内切球半径为r,则四体的体积”为: .
如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P.若PB=1,PD=3,则 的值为
的值为 
在梯形ABCD中,AB∥CD,AB=4,CD=2.E,F分别为AD,BC上点,且EF=3,EF∥AB,则梯形ABFE与梯形EFCD的面积比为 __
通过市场调查,得到某产品的资金投入 (万元)与获得的利润
(万元)与获得的利润 (万元)的数据,如下表所示:
(万元)的数据,如下表所示:
(1)根据上表提供的数据,用最小二乘法求线性回归直线方程 ;
;
(2)现投入资金 (万元),求估计获得的利润为多少万元.
(万元),求估计获得的利润为多少万元.
资金入 |
 |
 |
 |
 |
 |
利润 |
 |
3 |
 |
 |
 |
已知三角形ABC的三边长为a、b、c,且其中任意两边长均不相等.若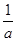 ,
,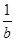 ,
,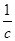 成等差数列.(1)比较
成等差数列.(1)比较 与
与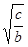 的大小,并证明你的结论;(2)求证B不可能是钝角
的大小,并证明你的结论;(2)求证B不可能是钝角
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出500件,量其内径尺寸,的结果如下表:
甲厂:
乙厂:
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
| |
甲 厂 |
乙 厂 |
合计 |
| 优质品 |
|
|
|
| 非优质品 |
|
|
|
| 合计 |
|
|
|
附: 

如图, 的角平分线
的角平分线 的延长线交它的外接圆于点
的延长线交它的外接圆于点
(Ⅰ)证明: ∽△
∽△ ;
;
(Ⅱ)若 的面积
的面积 ,求
,求 的大小.
的大小.
设函数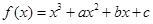 的图象如图所示,且与
的图象如图所示,且与 在原点相切,若函数的极小值为
在原点相切,若函数的极小值为 ,(1)求
,(1)求 的值;(2)求函数的递减区间.
的值;(2)求函数的递减区间.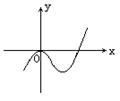
 的虚部为( )
的虚部为( )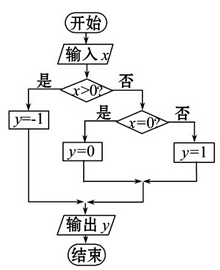

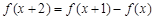 ,如果
,如果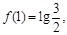


 粤公网安备 44130202000953号
粤公网安备 44130202000953号