如图,圆 与
与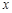 轴相切于点
轴相切于点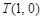 ,与
,与 轴正半轴
轴正半轴
交于两点 (
( 在
在 的上方),且
的上方),且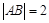 .
.
(Ⅰ)圆 的标准方程为 ;
的标准方程为 ;
(Ⅱ)过点 任作一条直线与圆
任作一条直线与圆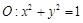 相交于
相交于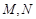 两点,下列三个结论:
两点,下列三个结论:
①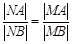 ; ②
; ②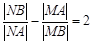 ;③
;③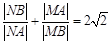 .
.
其中正确结论的序号是 .(写出所有正确结论的序号)
下列命题中_________为真命题.
① “A∩B=A”成立的必要条件是“A B”,
B”,
②“若x2+y2=0,则x,y全为0”的否命题,
③“全等三角形是相似三角形”的逆命题,
④“圆内接四边形对角互补”的逆否命题。
已知下列四个命题:
①“若 ,则
,则 互为倒数”的逆命题;
互为倒数”的逆命题;
②“面积相等的三角形全等”的否命题;
③“若 ,则方程
,则方程 有实根”的逆否命题;
有实根”的逆否命题;
④“若 ,则
,则 ”的逆否命题.
”的逆否命题.
其中真命题的是 .
有下列五个命题:
①若 =
= ,则
,则 之中至少有一个为空集;
之中至少有一个为空集;
②函数 的定义域为
的定义域为 ;
;
③集合 有两个元素;
有两个元素;
④函数 的图象是一直线;
的图象是一直线;
⑤不等式 的解集是
的解集是 .
.
其中错误命题的序号是 .
关于函数 下列结论:
下列结论:
① 的最小正周期是
的最小正周期是 ;
;
② 在区间
在区间 上单调递增;
上单调递增;
③函数 的图象关于点
的图象关于点 成中心对称图形;
成中心对称图形;
④将函数 的图象向左平移
的图象向左平移 个单位后与
个单位后与 的图象重合;
的图象重合;
其中成立的结论序号为 ▲ .
给出以下五个命题:①点 的一个对称中心
的一个对称中心
②设回时直线方程为 ,当变量x增加一个单位时,y大约减少2.5个单位
,当变量x增加一个单位时,y大约减少2.5个单位
③命题“在△ABC中,若 ,则△ABC为等腰三角形”的逆否命题为真命题
,则△ABC为等腰三角形”的逆否命题为真命题
④对于命题p:“ ”则
”则 “
“ ”
”
⑤设 ,
,  ,则“
,则“ ”是 “
”是 “ ” 成立的充分不必要条件.
” 成立的充分不必要条件.
不正确的是
给出以下五个命题:
①命题“ ,
, ”的否定是:“
”的否定是:“ ”.
”.
②已知函数 的图象经过点P(
的图象经过点P( ,1),则函数图象上过点P的切线斜率等于
,1),则函数图象上过点P的切线斜率等于
③ 是直线
是直线 和直线
和直线 垂直的充要条件.
垂直的充要条件.
④函数 在区间(0,1)上存在零点.
在区间(0,1)上存在零点.
⑤已知向量 与向量
与向量 的夹角为锐角,那么实数m的取值范围是(
的夹角为锐角,那么实数m的取值范围是( )
)
其中正确命题的序号是 .
有下列命题中假命题的序号是
①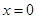 是函数
是函数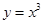 的极值点;
的极值点;
②三次函数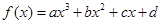 有极值点的充要条件是
有极值点的充要条件是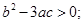
③奇函数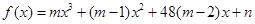 在区间
在区间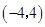 上单调递减.
上单调递减.
④若双曲线的渐近线方程为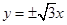 ,则其离心率为2.
,则其离心率为2.
给出下列四个命题,其中不正确命题的序号是 。
①若 ;②函数
;②函数 的图象关于x=
的图象关于x= 对称;③函数
对称;③函数 为偶函数,④函数
为偶函数,④函数 是周期函数,且周期为2
是周期函数,且周期为2 。
。
给出下列结论:
①命题“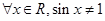 ”的否定是“
”的否定是“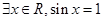 ”;
”;
②命题“有些正方形是平行四边形”的否定是“所有正方形不都是平行四边形”;
③命题“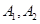 是对立事件”是命题“
是对立事件”是命题“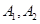 是互斥事件”的充分不必要条件;
是互斥事件”的充分不必要条件;
④若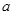 ,
,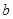 是实数,则“
是实数,则“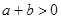 且
且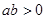 ”是“
”是“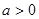 且
且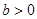 ”的必要不充分条件.
”的必要不充分条件.
其中正确结论的是 _________________.
给出下列结论:
①命题“ ”的否定是“
”的否定是“ ”;
”;
②命题“有些正方形是平行四边形”的否定是“所有正方形不都是平行四边形”;
③命题“ 是对立事件”是命题“
是对立事件”是命题“ 是互斥事件”的充分不必要条件;
是互斥事件”的充分不必要条件;
④若 ,
, 是实数,则“
是实数,则“ 且
且 ”是“
”是“ 且
且 ”的必要不充分条件.
”的必要不充分条件.
其中正确结论的是 _________________.
对于函数 ,现给出四个命题:
,现给出四个命题:
① 时,
时, 为奇函数;
为奇函数;
② 的图象关于
的图象关于 对称;
对称;
③ 时,方程
时,方程 有且只有一个实数根;
有且只有一个实数根;
④方程 至多有两个实数根
至多有两个实数根
其中正确命题的序号为 .
定义向量的运算
 (其中
(其中 为向量
为向量 的夹角),设
的夹角),设 为非零向量,则下列说法正确的是 .
为非零向量,则下列说法正确的是 .
① 是非负实数
是非负实数
②若向量 共线, 则有
共线, 则有 =0
=0
③若向量 垂直,则有
垂直,则有 =0
=0
④若 能构成三角形,则三角形面积
能构成三角形,则三角形面积
在下列命题中,
① ∈R,
∈R, +2
+2 +2≤0的否定;
+2≤0的否定;
②若m>0,则方程 +x-m=0有实根的逆命题;
+x-m=0有实根的逆命题;
③渐近线方程为y= x的双曲线的离心率为
x的双曲线的离心率为 ;
;
其中真命题的序号是__________________.