下列四个命题中,真命题的序号有 。(写出所有真命题的序号)
①若 则“
则“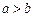 ”是“
”是“ ”成立的充分不必要条件;
”成立的充分不必要条件;
②当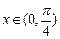 时,函数
时,函数 的最小值为2;
的最小值为2;
③命题“若 ,则
,则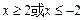 ”的否命题是“若
”的否命题是“若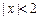 ,则
,则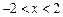 ”;
”;
④函数 在区间(1,2)上有且仅有一个零点。
在区间(1,2)上有且仅有一个零点。
给出下列四个结论:
①命题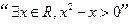 的否定是“
的否定是“ ”;
”;
②“若 则
则 ”的逆命题为真;
”的逆命题为真;
③函数 (x
(x )有3个零点;
)有3个零点;
④对于任意实数x,有 且x>0时,
且x>0时, 则x<0时
则x<0时
其中正确结论的序号是 。(填上所有正确结论的序号)
某医疗研究所为了检验某种血清预防感冒的作用,把 名使用血清的人与另外
名使用血清的人与另外 名未用血清的人一年中的感冒记录作比较,提出假设
名未用血清的人一年中的感冒记录作比较,提出假设 :“这种血清不能起到预防感冒的作用”,利用
:“这种血清不能起到预防感冒的作用”,利用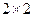 列联表计算得
列联表计算得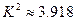 ,经查对临界值表知
,经查对临界值表知 .
.
对此,四名同学做出了以下的判断:
p:有 的把握认为“这种血清能起到预防感冒的作用”
的把握认为“这种血清能起到预防感冒的作用”
q:若某人未使用该血清,那么他在一年中有 的可能性得感冒
的可能性得感冒
r:这种血清预防感冒的有效率为
s:这种血清预防感冒的有效率为
则下列结论中,正确结论的序号是 .(把你认为正确的命题序号都填上)
(1) p∧﹁q; (2)﹁p∧q ;
(3)(﹁p∧﹁q)∧(r∨s); (4)(p∨﹁r)∧(﹁q∨s)
下列四个命题中
①“ ”是“函数
”是“函数 的最小正周期为
的最小正周期为 ”的充要条件;
”的充要条件;
②“ ”是“直线
”是“直线 与直线
与直线 相互垂直”的充要条件;
相互垂直”的充要条件;
③ 函数 的最小值为
的最小值为
其中假命题的为 (将你认为是假命题的序号都填上)
已知命题p:方程x2-mx+1=0有两个不等的正实数根;命题q:方程4x2+4(m-2)x+m2=0无实数根.若“p或q”为真,“p且q”为假,则m的取值范围是 .
已知命题p: ,命题q:
,命题q: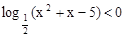 ,则
,则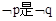 的
的
_ _条件(填充分不必要条件、必要不充分条件、充要条件)。
给出下列四个命题:
①命题:“设 ,若
,若 ,则
,则 或
或 ”
”
的否命题是“设 ,若
,若 ,则
,则 且
且 ”;
”;
②将函数 的图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),再向右平移
的图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),再向右平移 个单位长度,得到函数
个单位长度,得到函数 的图象;
的图象;
③用数学归纳法证明 时,从“
时,从“ ”到“
”到“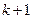 ”的证明,左边需增添的一个因式是
”的证明,左边需增添的一个因式是 ;
;
④函数 有两个零点.
有两个零点.
其中所有真命题的序号是 .