浙江省五校高三第一次联考(数学文)试题
观察下图:
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
…………
则第( )行的各数之和等于
| A.2010 | B.2009 | C.1006 | D.1005 |
今年“3·5”,某报社做了一次关于“什么是新时代的雷锋精神?”的调查,在A、B、C、D四个单位回收的问卷数依次成等差数列,共回收1000份,因报道需要,再从回收的问卷中按单位分层抽取容量为150的样本,若在B单位抽30份,则在D单位抽取的问卷是 份。
下列四个命题中,真命题的序号有 。(写出所有真命题的序号)
①若 则“
则“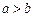 ”是“
”是“ ”成立的充分不必要条件;
”成立的充分不必要条件;
②当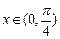 时,函数
时,函数 的最小值为2;
的最小值为2;
③命题“若 ,则
,则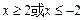 ”的否命题是“若
”的否命题是“若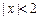 ,则
,则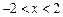 ”;
”;
④函数 在区间(1,2)上有且仅有一个零点。
在区间(1,2)上有且仅有一个零点。
 为坐标原点,
为坐标原点, ,
, .
. 的单调递增区间;
的单调递增区间; 的定义域为
的定义域为 ,值域为[2,5],求
,值域为[2,5],求 的值。
的值。 ,公比为
,公比为 ,
, ,
, 。
。 ,求证:
,求证: 。
。 为正实数,
为正实数, ,
, ,
, 。
。 ,则是否存在以
,则是否存在以 为三边长的三角形?请说明理由;
为三边长的三角形?请说明理由; ,试探索当存在以
,试探索当存在以 的取值范围。
的取值范围。 。
。 在其定义域内为单调递增函数,求实数
在其定义域内为单调递增函数,求实数 的取值范围;
的取值范围; ,且
,且 ,若在
,若在 上至少存在一点
上至少存在一点 ,使得
,使得 成立,求实数
成立,求实数 则
则 等于( )
等于( )


 的虚部是( )
的虚部是( )



 的部分图象如图所示,则
的部分图象如图所示,则 =( )
=( )



 ,则
,则 的值等于( )
的值等于( )

 满足
满足 ,则
,则 的最小值是( )
的最小值是( )

 ,
, ,
, 为坐标原点,点
为坐标原点,点 在
在 内,且
内,且 ,设
,设 ,则实数
,则实数 等于( )
等于( )


 ,则
,则 的值等于( )
的值等于( )



 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,若
,若 ,则实数
,则实数 的取值范围是( )
的取值范围是( )



 中,点
中,点 .对于某个正实数
.对于某个正实数 ,存在函数
,存在函数 (
( ),使得
),使得 (
( 为常数),这里点
为常数),这里点 的坐标分别为
的坐标分别为 ,则
,则



 的定义域是 。
的定义域是 。 中,角
中,角 所对应的边分别为
所对应的边分别为 ,若
,若 ,则
,则 等于 。
等于 。 。
。
 的导函数
的导函数 ,且
,且 的值为整数,当
的值为整数,当 时,
时, 。
。 :
: 在区间
在区间 上是减函数;命题
上是减函数;命题 :
: 是方程
是方程 的两个实根,不等式
的两个实根,不等式 对任意实数
对任意实数 恒成立;若
恒成立;若 为真,试求实数
为真,试求实数 的取值范围。
的取值范围。 粤公网安备 44130202000953号
粤公网安备 44130202000953号