广东省揭阳市高考一模(文)
如图,设A、B两点在河的两岸,一测量者在A的同侧,在所在的河岸
边选定一点C,测出AC的距离为50m,∠ ACB=45°,∠CAB=105°后,
就可以计算出A、B两点的距离为
A. m B.
m B. m C.
m C. m D.
m D. m
m
甲乙两人同时从A地出发往B地,甲在前一半时间以速度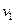 行驶,在后一半时间以速度
行驶,在后一半时间以速度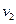 行驶,乙在前一半路程以速度
行驶,乙在前一半路程以速度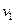 行驶,在后一半路程以速度
行驶,在后一半路程以速度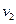 行驶,(
行驶,( ).则下列说法正确的是
).则下列说法正确的是
| A.甲先到达B地 | B.乙先到达B地 |
| C.甲乙同时到达B地 | D.无法确定谁先到达B地 |
随机抽取某中学甲、乙两个班各10名同学,测量他们的身高(单位:cm)获得身高数据的茎叶图如下图甲,在样本的20人中,记身高在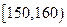 ,
,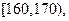
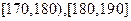 的人数依次为
的人数依次为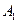 、
、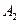 、
、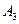 、
、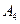 .图乙是统计样本中身高在一定范围内的人数的算法流程图,由图甲可知甲、乙两班中平均身高较高的是 班;图乙输出的
.图乙是统计样本中身高在一定范围内的人数的算法流程图,由图甲可知甲、乙两班中平均身高较高的是 班;图乙输出的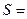 .(用数字作答)
.(用数字作答)
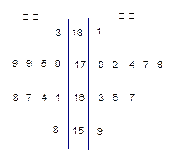
图甲 图乙
(几何证明选做题)如图,已知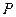 是
是 外一点,
外一点,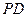 为
为 的切线,
的切线,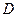 为切点,割线PEF经过圆心
为切点,割线PEF经过圆心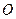 ,若
,若 ,
, ,则圆
,则圆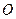 的半径长为 、
的半径长为 、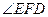 的度
的度
数为 .

右图为一简单组合体,其底面ABCD为正方形,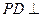 平面
平面 ,
, ,且
,且 ="2" .
="2" .
(1)答题卡指定的方框内已给出了该几何体的俯视图,请在方框
内画出该几何体的正(主)视图和侧(左)视图;
(2)求四棱锥B-CEPD的体积;
(3)求证: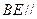 平面
平面 .
.
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)已知喜爱打篮球的10位女生中, 还喜欢打羽毛球,
还喜欢打羽毛球,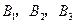 还喜欢打乒乓球,
还喜欢打乒乓球,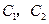 还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求
还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求 和
和 不全被选中的概率.
不全被选中的概率.
下面的临界值表供参考:
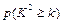 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)
在平面直角坐标系中,已知向量 (
( ),
),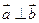 ,动点
,动点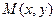 的轨迹为T.
的轨迹为T.
(1)求轨迹T的方程,并说明该方程表示的曲线的形状;
(2)当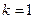 时,已知
时,已知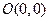 、
、 ,试探究是否存在这样的点
,试探究是否存在这样的点 :
: 是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积
是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积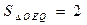 ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由.
已知曲线 :
: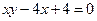 ,数列
,数列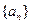 的首项
的首项 ,且当
,且当 时,点
时,点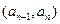 恒在曲线
恒在曲线 上,数列
上,数列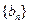 满足
满足 .
.
(1)试判断数列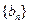 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;
(2)求数列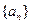 和
和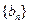 的通项公式;
的通项公式;
(3)设数列 满足
满足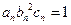 ,试比较数列
,试比较数列 的前n项和
的前n项和 与2的大小.
与2的大小.
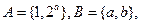 若
若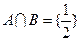 ,则
,则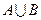 为
为
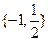

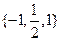
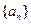 是等比数列,且
是等比数列,且 ,
,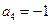 ,则
,则 为
为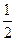
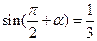 ,则
,则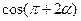 的值为
的值为 B.
B. C.
C.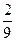 D
D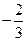
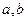 是两条直线,
是两条直线,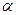 、
、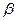 是两个平面,则下列命题中错误的是
是两个平面,则下列命题中错误的是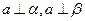 ,则
,则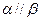
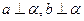 ,则
,则
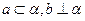 则
则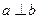
 则
则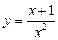 (
( )上横坐标为1的点的切线方程为
)上横坐标为1的点的切线方程为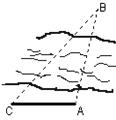
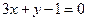
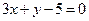
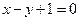
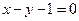
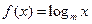 的反函数的图象过点
的反函数的图象过点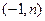 ,则
,则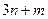 的最小值是C
的最小值是C
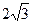
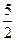
 ,则△ABC的内角A等于
,则△ABC的内角A等于
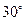
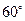


 ,则不等式组
,则不等式组 对应的平面区域为
对应的平面区域为
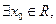
 ”的否定为 .
”的否定为 . 上一点P到右焦点的距离是长轴两端点到右焦点距离的等差中项,则P点的坐标为 .
上一点P到右焦点的距离是长轴两端点到右焦点距离的等差中项,则P点的坐标为 . 的参数方程为
的参数方程为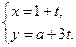 (
( 为参数),直线
为参数),直线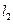 的方程为
的方程为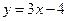 ,若直线
,若直线 ,则实数
,则实数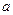 的值为 .
的值为 . ,
, ,且
,且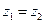 .
.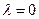 且
且 ,求
,求 的值;
的值;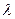 =
=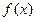 ,求
,求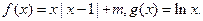

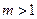 时,求函数
时,求函数 在
在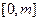 上的最大值;
上的最大值; ,若函数
,若函数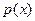 有零点,求
有零点,求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号