若方程 在[0,2]上有解,则实数m的取值范围为( )
在[0,2]上有解,则实数m的取值范围为( )
A. |
B. |
C. |
D. |
(本小题满分13分)
在一条笔直的工艺流水线上有 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为 ,
, ,
, ,每个工作台上有若干名工人.现要在
,每个工作台上有若干名工人.现要在 与
与 之间修建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
之间修建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
(Ⅰ)若每个工作台上只有一名工人,试确定供应站的位置;
(Ⅱ)设工作台从左到右的人数依次为 ,
, ,
, ,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
图5
(本小题满分13分)
在一条笔直的工艺流水线上有 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为 ,
, ,
, ,
, ,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
(Ⅰ)若 ,每个工作台上只有一名工人,试确定供应站的位置;
,每个工作台上只有一名工人,试确定供应站的位置;
(Ⅱ)若 ,工作台从左到右的人数依次为
,工作台从左到右的人数依次为 ,
, ,
, ,
, ,
, ,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
对于大于1的自然数 的
的 次幂可用奇数
次幂可用奇数
进行如图所示的“分裂”,仿此,记 的“分裂”
的“分裂”
中的最小数为 ,而
,而 的“分裂”中最大的数
的“分裂”中最大的数
是 ,则
,则 _____.
_____.
(本小题满分16分)已知函数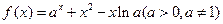 .
.
(Ⅰ)当 时,求证:函数
时,求证:函数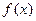 在
在 上单调递增;
上单调递增;
(Ⅱ)若函数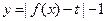 有三个零点,求
有三个零点,求 的值;
的值;
(Ⅲ)若存在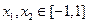 ,使得
,使得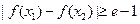 ,试求
,试求 的取值范围.
的取值范围.
本题共有2个小题,第1小题满分8分,第2小题满分8分.已知函数 (其中
(其中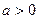 且
且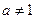 ,
,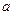 为实数常数).
为实数常数).
(1)若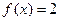 ,求
,求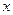 的值(用
的值(用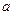 表示);
表示);
(2)若 且
且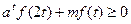 对于
对于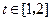 恒成立,求实数m的取值范围(用
恒成立,求实数m的取值范围(用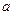 表示).
表示).
对于任意实数 ,符号[
,符号[ ]表示
]表示 的整数部分,即[
的整数部分,即[ ]是不超过
]是不超过 的最大整数”。在实数轴R(箭头向右)上[
的最大整数”。在实数轴R(箭头向右)上[ ]是在点
]是在点 左侧的第一个整数点,当
左侧的第一个整数点,当 是整数时[
是整数时[ ]就是
]就是 。这个函数[
。这个函数[ ]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。
]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。
那么 = .
= .