[湖南]湖南省高考适应性测试数学(文)
一位母亲记录了儿子 岁至
岁至 岁的身高,数据如下表,由此建立的身高与年龄的回归模型为
岁的身高,数据如下表,由此建立的身高与年龄的回归模型为 .用这个模型预测这个孩子
.用这个模型预测这个孩子 岁时的身高,则正确的叙述是
岁时的身高,则正确的叙述是
| 年龄/岁 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
身高/ |
94.8 |
104.2 |
108.7 |
117.8 |
124.3 |
130.8 |
139.0 |
A.身高一定是 B.身高在
B.身高在 以上
以上
C.身高在 左右 D.身高在
左右 D.身高在 以下
以下
(本小题满分12分)
甲,乙两人进行射击比赛,每人射击 次,他们命中的环数如下表:
次,他们命中的环数如下表:
| 甲 |
5 |
8 |
7 |
9 |
10 |
6 |
| 乙 |
6 |
7 |
4 |
10 |
9 |
9 |
(Ⅰ)根据上表中的数据,判断甲,乙两人谁发挥较稳定;
(Ⅱ)把甲6次射击命中的环数看成一个总体,用简单随机抽样方法从中抽取两次命中的环数组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过 的概率.
的概率.
(本小题满分13分)
在一条笔直的工艺流水线上有 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为 ,
, ,
, ,每个工作台上有若干名工人.现要在
,每个工作台上有若干名工人.现要在 与
与 之间修建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
之间修建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
(Ⅰ)若每个工作台上只有一名工人,试确定供应站的位置;
(Ⅱ)设工作台从左到右的人数依次为 ,
, ,
, ,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
图5
(本小题满分13分)
已知首项不为零的数列 的前
的前 项和为
项和为 ,若对任意的
,若对任意的 ,
, ,都有
,都有 .
.
(Ⅰ)判断数列 是否为等差数列,并证明你的结论;
是否为等差数列,并证明你的结论;
(Ⅱ)若数列 的第
的第 项
项 是数列
是数列 的第
的第 项
项 ,且
,且 ,
, ,求数列
,求数列 的前
的前 项和
项和 .
.
 ,
, ,则
,则






 ,则下列判断正确的是
,则下列判断正确的是 假
假 真
真 的一个单调递增区间是
的一个单调递增区间是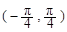



 ,
, 的夹角为
的夹角为 ,且
,且 ,则
,则 =" "
=" "



 所示,其输出结果
所示,其输出结果





 的图象在
的图象在 处的切线
处的切线 过点
过点 ,且
,且 相交,则点
相交,则点 与圆
与圆 的位置关系是
的位置关系是  .设实数
.设实数 ,
, 满足约束条件
满足约束条件 ,
, 的取值范围为
的取值范围为



 .
. 的方程为
的方程为 ,则点
,则点 到直线
到直线 到
到 之间.现用分数法进行优选,则第二次试点的温度为
之间.现用分数法进行优选,则第二次试点的温度为  .
. ,函数
,函数 的图象是一条连续不断的曲线,则
的图象是一条连续不断的曲线,则 .
.
 )如图
)如图 所示,则此几何体的表面积是
所示,则此几何体的表面积是  .
.

 ”:表示若干个数相乘,例如:
”:表示若干个数相乘,例如: .记
.记 ,
, 为数列
为数列 中的第
中的第 项.
项. ,则
,则 ;
; ,则
,则 .
. 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,向量
,向量 ,
, ,且
,且 .
. ,
, ,求
,求 ,
, 是圆
是圆 的的直径,点
的的直径,点 是弧
是弧 ,
, 分别是
分别是 ,
, 的中点,
的中点,
 .
.
 与
与 平面
平面 .
.
 中,
中, ,
, ,点
,点 ,
, 满足
满足 ,
, ,点
,点 是
是 关于原点的对称点,直线
关于原点的对称点,直线 与
与 相交于点
相交于点 .
. 的直线与点
的直线与点 ,
, 两点,求
两点,求 的面积的最大值.
的面积的最大值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号