(本小题满分12分)
某地区上年度电价为0.8元/kW·h,年用电量为akW·h,本年度计划将电价降到0.55元/kW·h至0.75元/kW·h之间,而用户期望电价为0.4元/kW·h,经测算,下调电价后新增的用电量与实际电价和用户期望电价的差成反比(比例系数为k).该地区电力的成本价为0.3元/kW·h.
(Ⅰ)写出本年度电价下调后,电力部门的收益y与实际电价x的函数关系式;
(Ⅱ)设k=0.2a,当电价最低定为多少时仍可保证电力部门的收益比上年至少增长20%?
(注:收益=实际用电量×(实际电价-成本价))
(本小题满分12分)
. 设 R, 且
R, 且 , 定义在区间
, 定义在区间 内的函数
内的函数 是奇函数.
是奇函数.
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)讨论函数 的单调性,并加以证明.
的单调性,并加以证明.
(本题8分)某村计划建造一个室内面积为800 的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3 宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
(本小题满分12分)
某汽车公司购买了4辆大客车,每辆200万元,用于长途客运,预计每辆车每年收入约100万元,每辆车每年各种费用约为16万元,且从第二年开始每年比上一年所需费用要增加16万元.
(1)写出4辆车运营的总利润 (万元)与运营年数
(万元)与运营年数
 的函数关系式;
的函数关系式;
(2)这4辆车运营多少年,可使年平均运营利润最大?
如图,两木块的的质量分别是m1和 m2,两轻弹簧的劲度系数分别为k1和k2,上面的木块压上面的弹簧上,整个系处于平衡状态,现缓慢向上提上面的木块直到它刚离开上面的弹簧,在这个过程中,下面的木块移动的距离为:( )

A. |
B. |
C. |
D. |
已知二次函数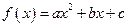 和“伪二次函数”
和“伪二次函数”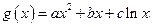 (
(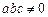 ),
),
(1)证明:只要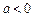 ,无论
,无论 取何值,函数
取何值,函数 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(2)在同一函数图像上任意取不同两点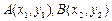 ,线段
,线段 中点为
中点为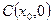 ,记直线
,记直线 的斜率为
的斜率为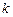 ,
,
1对于二次函数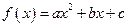 ,求证:
,求证: ;
;
2对于“伪二次函数”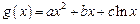 ,是否有1同样的性质?证明你的结论.
,是否有1同样的性质?证明你的结论.
(本小题满分16分)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是等腰梯形,其中高0.5米,AB=1米, CD=2a(a> )米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.
)米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.
(1)设MN与AB之间的距离为x米,试将三角通风窗EMN的通风面积S(平方米)表示成关于x的函数 ;
;
(2)当MN与AB之间的距离为多少米时,三角通风窗EMN的通风面积最大?并求出这个最大面积.