高中数学三面角、直三面角的基本性质解答题

已知函数f(x)＝是奇函数．
(1)求实数m的值；
(2)若函数f(x)在区间[－1，a－2]上单调递增，求实数a的取值范围．

已知函数，．             
（1）求函数的定义域；
（2）当时，总有成立，求的取值范围．

设0≤x≤2，求函数y=的最大值和最小值．

已知函数（其中）.
（Ⅰ）求的单调区间；
（Ⅱ）求在上的最大值与最小值.

设函数，曲线在点处的切线方程为
，求的解析式.

已知函数（），将的图象向右平移两个单位，得到函数的图象，函数与函数的图象关于直线对称.
（1）求函数和的解析式；
（2）若方程在上有且仅有一个实根，求的取值范围；
（3）设，已知对任意的恒成立，求的取值范围.

(14分)已知函数的图象过原点，且关于点（-1,1）成中心对称．（1）求函数的解析式；（2） 若数列(nÎN*)满足：，求数列的通项公式.

（本小题满分12分）
学校要建一个面积为392 m²的长方形游泳池，并且在四周要修建出宽为2m和4 m的小路（如图所示）。
问游泳池的长和宽分别为多少米时，占地面积最小？并求出占地面积的最小值。

．(本小题满分14分)已知函数对任意实数均有，当时，是正比例函数，当时，是二次函数，且在时取最小值。
（1）证明：；
（2）求出在的表达式；并讨论在的单调性。

(本题满分14分，第1小题满分7分，第2小题满分7分)
为了研究某种癌细胞的繁殖规律和一种新型抗癌药物的作用，将癌细胞注入一只小白鼠体内进行实验，经检测，癌细胞的繁殖规律与天数的关系如下表.已知这种癌细胞在小白鼠体内的个数超过时小白鼠将会死亡，注射这种抗癌药物可杀死其体内癌细胞的.

天数	1	2	3	4	5	6	7	…
癌细胞个数	1	2	4	8	16	32	64	…

(1)要使小白鼠在实验中不死亡，第一次最迟应在第几天注射该种药物？(精确到1天)
(2)若在第10天，第20天，第30天，……给小白鼠注射这种药物，问第38天小白鼠是否仍然存活？请说明理由.

（文）函数，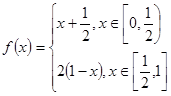
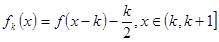定义的第阶阶梯函数，其中 ，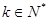
的各阶梯函数图像的最高点，
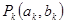（1）直接写出不等式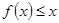的解；
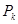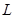（2）求证：所有的点在某条直线上．

（本题共3小题，满分18分。第1小题满分4分，第2小题满分７分，第3小题７分）
对定义在上，并且同时满足以下两个条件的函数称为函数．
① 对任意的，总有；
② 当时，总有成立．
已知函数与是定义在上的函数．
（1）试问函数是否为函数？并说明理由；
（2）若函数是函数，求实数的值；
（3）在（2）的条件下，是否存在实数，使方程恰有两解？若存在，求出实数的取值范围；若不存在，请说明理由．

（本小题满分12分）设，其中为正实数
（1）当时，求的极值点；
（2）若为上的单调函数，求的取值范围。

已知二次函数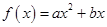(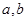是常数，且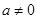)满足条件：，且方程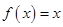有两个相等实根．
(1)求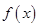的解析式；
(2)是否存在实数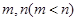，使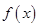的定义域和值域分别为和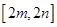？若存在，求出的值；若不存在，说明理由．

(12分)已知函数是定义在上的增函数，对于任意的，都有，且满足.
（1）求的值;   
（2）求满足的的取值范围．