为了在夏季降温和冬季供暖时减少能源损耗,房屋的房顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用为C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= (0
(0 x
x 10),若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
10),若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
已知:在函数 的图象上,以
的图象上,以 为切点的切线的倾斜角为
为切点的切线的倾斜角为 .
.
(Ⅰ)求 ,
, 的值;
的值;
(Ⅱ)是否存在最小的正整数 ,使得不等式
,使得不等式 对于
对于 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数 ;如果不存在,请说明理由;
;如果不存在,请说明理由;
(Ⅲ)求证: (
( ,
, ).
).
已知 是定义在
是定义在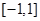 上的奇函数,且
上的奇函数,且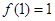 ,若
,若 ,
, 有
有 恒成立.
恒成立.
(1)判断 在
在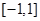 上是增函数还是减函数,并证明你的结论;
上是增函数还是减函数,并证明你的结论;
(2)若 对所有
对所有 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
已知函数 ,在
,在 时取得极值.
时取得极值.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(Ⅲ)若 ,是否存在实数b,使得方程
,是否存在实数b,使得方程 在区间
在区间 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
已知函数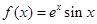 .
.
⑴ 求函数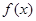 的单调区间;
的单调区间;
⑵ 如果对于任意的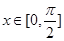 ,
,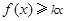 总成立,求实数
总成立,求实数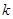 的取值范围;
的取值范围;
⑶ 设函数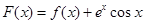 ,
,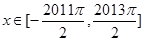 . 过点
. 过点 作函数
作函数 图像的所有切线,令各切点的横坐标构成数列
图像的所有切线,令各切点的横坐标构成数列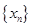 ,求数列
,求数列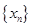 的所有项之和
的所有项之和 的值.
的值.
已知函数f(x)= (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式f(x)<  .
.
已知函数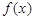 的定义域为
的定义域为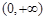 ,若
,若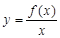 在
在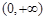 上为增函数,则称
上为增函数,则称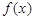 为“一阶比增函数”;若
为“一阶比增函数”;若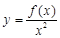 在
在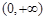 上为增函数,则称
上为增函数,则称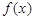 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为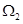 .
.
(Ⅰ)已知函数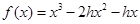 ,若
,若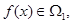 且
且 ,求实数
,求实数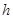 的取值范围;
的取值范围;
(Ⅱ)已知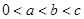 ,
,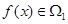 且
且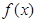 的部分函数值由下表给出,
的部分函数值由下表给出,
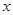 |
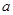 |
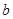 |
 |
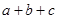 |
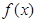 |
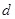 |
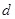 |
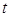 |
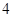 |
求证: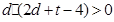 ;
;
(Ⅲ)定义集合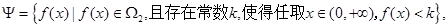
请问:是否存在常数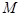 ,使得
,使得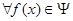 ,
,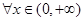 ,有
,有 成立?若存在,求出
成立?若存在,求出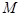 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
进货原价为80元的商品400个,按90元一个售出时,可全部卖出.已知这种商品每个涨价一元,其销售数就减少20个,问售价应为多少时所获得利润最大?