在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数f(x)的图象恰好通过n(n∈N*)个整点,则称函数f(x)为n阶整点函数.有下列函数:
①f(x)=x+ (x>0);②g(x)=x3;
(x>0);②g(x)=x3;
③h(x)=( )x;④φ()=lnx.
)x;④φ()=lnx.
其中是一阶整点函数的是( )
| A.①②③④ | B.①③④ |
| C.④ | D.①④ |
设关于 的函数
的函数 ,其中
,其中 为
为 上的常数,若函数
上的常数,若函数 在
在 处取得极大值
处取得极大值
(1)求实数 的值
的值
(2)若函数 的图像与直线
的图像与直线 有两个交点,求实数
有两个交点,求实数 的取值范围
的取值范围
(3)设函数 ,若对任意的
,若对任意的 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元)
(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式
(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润约为多少万元。(精确到1万元)。
(本题满分12分,(Ⅰ)小问6分,(Ⅱ)小问6分.)
两个二次函数 与
与 的图象有唯一的公共点
的图象有唯一的公共点 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)设 ,若
,若 在
在 上是单调函数,求
上是单调函数,求 的范围,并指出是单调递增函数,还是单调递减函数.
的范围,并指出是单调递增函数,还是单调递减函数.
某种动物繁殖量 (只)与时间
(只)与时间 (年)的关系为
(年)的关系为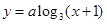 ,设这种动物第2年有100只,到第8年它们将发展到( )
,设这种动物第2年有100只,到第8年它们将发展到( )
| A.200只 | B.300只 | C.400只 | D.500只 |
设
,已知函数
.
(Ⅰ)当
时,讨论函数
的单调性;
(Ⅱ)当
时,称
为
关于
的加权平均数.
(1)判断
是否成等比数列,并证明
;
(2)
的几何平均数记为
.称
为
的调和平均数,记为
.若
,求
的取值范围.
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
| A.y=cos 2x,x∈R |
| B.y=log2|x|,x∈R且x≠0 |
C.y=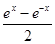 ,x∈R ,x∈R |
| D.y=x3+1,x∈R |