[湖北]2012届湖北省黄冈市浠水县高三9月联考理科数学
“a>0”是“ >0”的( )
>0”的( )
| A.充分不必要条件 | B.必要不充分条件 |
C.充要条件  |
D.既不充分也不必要条件 |
来源:2012届湖北省黄冈市浠水县高三9月联考理科数学
若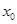 是方程式
是方程式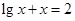 的解,则
的解,则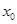 属于区间( )
属于区间( )
| A.(0,1) | B.(1,1.25) |
| C.(1.25,1.75) | D.(1.75,2) |
来源:2012届湖北省黄冈市浠水县高三9月联考理科数学
(理数)将边长为1m正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记 ,
, 则S的最小值是_______
则S的最小值是_______
来源:2012届湖北省黄冈市浠水县高三9月联考理科数学
(理数)某商场销售 某种商品的经验表明,该商品每日的销售量
某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满
(单位:元/千克)满 足关系式
足关系式 ,其中
,其中 ,
, 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克
(Ⅰ) 求 的值;
的值;
(Ⅱ) 若该商品的成品为3元/千克, 试确定销售价格 的值,使商场每日销售该
的值,使商场每日销售该 商品所获得的利润最大.
商品所获得的利润最大.
来源:2012届湖北省黄冈市浠水县高三9月联考理科数学
(12分 ) .已知函数y=
) .已知函数y= f(x)=
f(x)= (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(1)试求函数f(x)的解析式
(2)问函数f(x)图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说 明理由.
明理由.
来源:2012届湖北省黄冈市浠水县高三9月联考理科数学
定义在R上的增函数y=f(x)对任意x,y R都有f(x+y)=f(x)+f(y),则
R都有f(x+y)=f(x)+f(y),则
(1)求f(0) (2) 证明:f(x)为奇函数
(3)若 对任意
对任意 恒成立,求实数k的取值范围
恒成立,求实数k的取值范围
来源:2012届湖北省黄冈市浠水县高三9月联考理科数学
 ,
, ,则
,则 ( )
( )



 的值域是( )
的值域是( )



 是周期为2的奇函数,当
是周期为2的奇函数,当 时,
时, ,则
,则 ( )
( )



 为定义在
为定义在 上的奇函数,当
上的奇函数,当 时,
时, (
( 为常数),则
为常数),则 ( )
( ) 在点
在点 处的切线方程是
处的切线方程是 ,则( )
,则( )



 单调递增的函数是( )
单调递增的函数是( )



 的图象关于直线y=x对称的图象像
的图象关于直线y=x对称的图象像 大致是( )
大致是( )
 与曲线
与曲线 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )


 ______
______ ,一元二次方程
,一元二次方程 有整数根的充要条件是
有整数根的充要条件是 =
=  与曲线
与曲线 有四个交点,则
有四个交点,则 的取值范围是
的取值范围是  对任意x
对任意x 恒成立,则实数m的取值范
恒成立,则实数m的取值范 围是_______
围是_______ 有最小正周期4,且
有最小正周期4,且 时,
时, 。求
。求 上的解析
上的解析 式
式 ,曲线在点M处的切线恰好与直线
,曲线在点M处的切线恰好与直线 垂直
垂直 的值
的值 )若函数
)若函数 的取值范围。
的取值范围。 ,
, .
. [h(x)]
[h(x)] ,求F(x)的单调区间与极值;
,求F(x)的单调区间与极值; ,解关于x的方程
,解关于x的方程 ;
; ,证明:
,证明: .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号