（理数）某商场销售
某种商品的经验表明，该商品每日的销售量
(单位：千克)与销售价格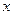
(单位：元/千克)满
足关系式
，其中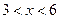
，
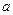为常数，已知销售价格为5元/千克时，每日可售出该商品11千克
(Ⅰ) 求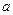的值；
(Ⅱ) 若该商品的成品为3元/千克, 试确定销售价格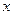的值,使商场每日销售该商品所获得的利润最大．
相关试题
，
。
.
满足条件：（1）当
时，都有
且
成立;（2）当
时，
；（3）
在
上的最小值为0.
的值及
，使得存在
，只要
，就有
成立.
上的函数
满足：
对任意
、
恒成立，当
时，
.
，解关于
的不等式
；
，且不等式
对任意
恒成立.求实数
的取值范围.
是奇函数，
在区间
上是单调递减函数；
对任意
的取值范围.
的不等式
的解集是
，函数
的定义域是
，若
.求实数
的取值范围.推荐套卷
（理数）某商场销售某种商品的经验表明，该商品每日的销售量(单位：千克)与销售价格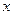(单位：元/千克)满足关系式，其中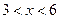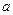，为常数，已知销售价格为5元/千克时，每日可售出该商品11千克
(Ⅰ) 求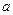的值；
(Ⅱ) 若该商品的成品为3元/千克, 试确定销售价格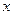的值,使商场每日销售该商品所获得的利润最大．
粤公网安备 44130202000953号