设关于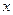 的函数
的函数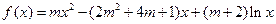 ,其中
,其中 为
为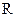 上的常数,若函数
上的常数,若函数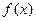 在
在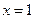 处取得极大值
处取得极大值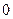
(1)求实数 的值
的值
(2)若函数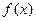 的图像与直线
的图像与直线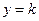 有两个交点,求实数
有两个交点,求实数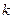 的取值范围
的取值范围
(3)设函数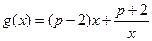 ,若对任意的
,若对任意的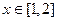 ,
,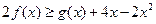 恒成立,求实数
恒成立,求实数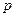 的取值范围.
的取值范围.
相关知识点
推荐套卷
设关于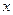 的函数
的函数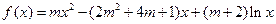 ,其中
,其中 为
为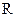 上的常数,若函数
上的常数,若函数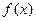 在
在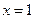 处取得极大值
处取得极大值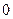
(1)求实数 的值
的值
(2)若函数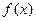 的图像与直线
的图像与直线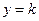 有两个交点,求实数
有两个交点,求实数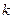 的取值范围
的取值范围
(3)设函数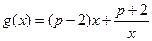 ,若对任意的
,若对任意的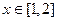 ,
,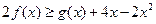 恒成立,求实数
恒成立,求实数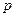 的取值范围.
的取值范围.