(本小题共12分)
在直角坐标系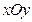 中,动点P到两定点
中,动点P到两定点 ,
,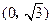 的距离之和等于4,设动点P的轨迹为
的距离之和等于4,设动点P的轨迹为 ,过点
,过点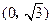 的直线与
的直线与 交于A,B两点.
交于A,B两点.
(1)写出 的方程;
的方程;
(2)设d为A、B两点间的距离,d是否存在最大值、最小值;若存在,求出d的最大值、最小值.
推荐套卷
(本小题共12分)
在直角坐标系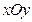 中,动点P到两定点
中,动点P到两定点 ,
,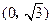 的距离之和等于4,设动点P的轨迹为
的距离之和等于4,设动点P的轨迹为 ,过点
,过点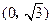 的直线与
的直线与 交于A,B两点.
交于A,B两点.
(1)写出 的方程;
的方程;
(2)设d为A、B两点间的距离,d是否存在最大值、最小值;若存在,求出d的最大值、最小值.