（本小题满分14分）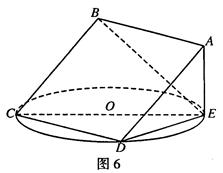
如图6，正方形ABCD所在平面与圆O所在平面
相交于CD，线段CD为圆O的弦，AE垂直于圆
O所在平面，垂足E是圆O上异于C、D的点，
AE＝3，圆O的直径为9．
（1）求证：平面 ABCD ⊥平面 ADE；
（2）求二面角D—BC—E的平面角的正切值．
A是锐角,求
的值；
.
,求
的值.
，且
．
、
的值；
、
、
的值．推荐套卷
（本小题满分14分）
如图6，正方形ABCD所在平面与圆O所在平面
相交于CD，线段CD为圆O的弦，AE垂直于圆
O所在平面，垂足E是圆O上异于C、D的点，
AE＝3，圆O的直径为9．
（1）求证：平面 ABCD ⊥平面 ADE；
（2）求二面角D—BC—E的平面角的正切值．
粤公网安备 44130202000953号