（本小题共12分）
甲、乙两个射手进行射击训练，甲击中目标的概率为
，乙击中目标的概率为
，每人各射击两发子弹为一个“单位射击组”，若甲击中目标的次数比乙击中目标的次数多，则称此组为“单位进步组”.
（1）求一个“单位射击组”为“单位进步组”的概率；
（2）记完成三个“单位射击组”后出现“单位进步组”的次数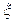
，求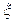的分布列与数学期望.
是各棱长为5的正三棱柱，
,
分别是
,
的中点，则平面
与平面
的距离为多少
的值域
的值域
次成功，则第
次也成功的概率为
，当第
，若首次试验成功和失败的概率都是
次试验成功的概率
的所有棱长都是
，
分别是
,
的中点
∥平面
（2）求证
平面推荐套卷
（本小题共12分）
甲、乙两个射手进行射击训练，甲击中目标的概率为，乙击中目标的概率为，每人各射击两发子弹为一个“单位射击组”，若甲击中目标的次数比乙击中目标的次数多，则称此组为“单位进步组”.
（1）求一个“单位射击组”为“单位进步组”的概率；
（2）记完成三个“单位射击组”后出现“单位进步组”的次数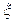，求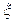的分布列与数学期望.
粤公网安备 44130202000953号